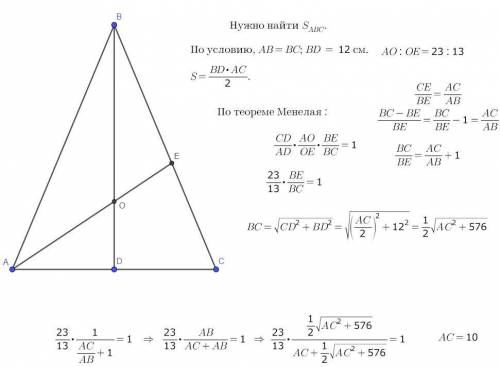
Пусть О — точка пересечения высоты BD и биссектрисы AE.
AO : OE = 23 : 13, BD = 12 см. По теореме Менелая для треугольника АЕС имеем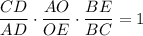 
. Поскольку треугольник ABC равнобедренный, то BD является биссектрисой и медианой, т.е. AD = DC, тогда 
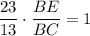(1).
По свойству биссектрисы: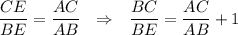 
.
По теореме Пифагора из прямоугольного треугольника BDC:
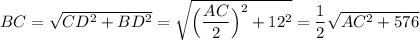
Подставляем в равенство (1), получим уравнение относительно АС.
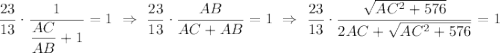
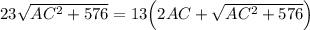
Решаете как иррациональное уравнение, возводите два раза обе части уравнения и вы должны придти к биквадратному уравнению , получите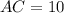 
см.
Площадь треугольника: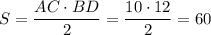 
см²
ответ: 60 см².
Задачи на второй признак равенства треугольников
Треугольники
Посмотрев данный видеоурок, все желающие смогут получить представление о теме «Задачи на второй признак равенства треугольников». В ходе этой лекции учащимся предстоит вспомнить, повторить и научиться применять все о втором признаке равенства треугольников. Учитель подробно разберет и решит несколько задач по этой теме.
Сначала вспомним, что две фигуры называются равными, если их можно совместить наложением. Однако очень трудно сравнивать фигуры по определению, поэтому мы введем признаки равенства треугольников – по некоторым элементам.
Объяснение: