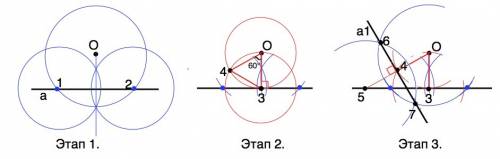
Все этапы построения показаны на рисунках приложения.
Этап 1) Вне прямой а отмечаем точку О.
Из О на прямой а с циркуля произвольного традиуса отмечаем точки 1 и 2.
Из этих точек, как из центров, проводим две окружности так, чтобы они пересеклись по разные стороны от прямой а. Соединим точки пересечения окружностей прямой. Точку пересечения этой прямой с прямой а обозначим 3.
–––––
Этап 2) Из т.О радиусом, равным длине отрезка О3, проведем окружность.
Из т.3 тем же радиусом на проведенной окружности отметим точку 4. Стороны треугольника 4О3 равны радиусу, он - равносторонний, поэтому угол 4О3=60°
––––––––––
Этап 3) Продлим радиус О4 (удобно продлить на его длину) и отметим точку 5. Для данной задачи точка 5 будет лежать на прямой а, т.к. в прямоугольном ∆ 3О5 с острым углом при т.О=60° гипотенуза О5 равна двум радиусам ( двум катетам О3).
Общепринятым построения перпендикуляра к прямой проведем прямую, проходящую через т.4 и перпендикулярную к отрезку О5 (чертим окружности с центрами в т.О и т.5, точки их пересечения 6 и 7 соединяем). Отмечаем прямую а1. Она перпендикулярна радиусу О4 и повёрнута вокруг т.О на 60° по часовой стрелке.
Условие написано очень не понятно.
Что такое САО?Треугольник?Угол?
Если угол,то <САО никак не может быть равен 2DBO
Будем считать,что САО и DBO углы<) и они равны между собой
Заданию три недели,его никто не решил,т к не понятно условие
Итак,пересеклись два о резка,по условию задачи
АО=ВО;<САО=<ОВD
<АОС=<DOB,как вертикальные,образованные при пересечении двух отрезков
Следовательно,треугольники САО и DBO равны между собой по второму признаку равенства треугольников,если сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащим к ней углам другого треугольника,то эти треугольники равны между собой,а значит
АО=ОВ=5 см
DO=OC=7 cм
DB=AC=6 cм
Периметр-сумма всех сторон треугольника
Периметр САО=5+7+6=18 см
Объяснение:
Сегме́нт круга — часть круга, ограниченная дугой окружности и её хордой или секущей
Объяснение: