На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили
точку D так, что AD = AC и точки A находится между точками B и D. Найдите величину угла ,ADС
если угол ABC равен 32градуса

Question

Геометрия: На продолжении стороны AB равнобедренного треугольника ABC с основанием AC отметили точку D так, что AD = AC и точки A находится между точками B и D. Найдите величину угла ,ADС если угол ABC равен 32градуса

Valeria25092006 · Accepted Answer

Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.

Рассмотрим ∆КРР₁ и ∆КММ₁.

Угол МКМ₁ – общий;

Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)

Следовательно ∆КРР₁~∆КММ₁ по двум углам.

Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.

Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:

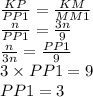
$\frac{KP}{ PP1} = \frac{KM }{MM1} \\ \frac{n}{PP1} = \frac{3n}{9} \\ \frac{n}{3n} = \frac{PP1}{9} \\ 3 \times PP1 = 9 \\ PP1 = 3$

ответ: 3 см

Через кінець К відрізка КМ проведено площину а. Точка Р належить відрізку КМ, причому КР:РМ=1:2. Чер

MOGZ ответил