Площадь полной поверхности призмы равна сумме площади боковой поверхности и площади двух оснований.
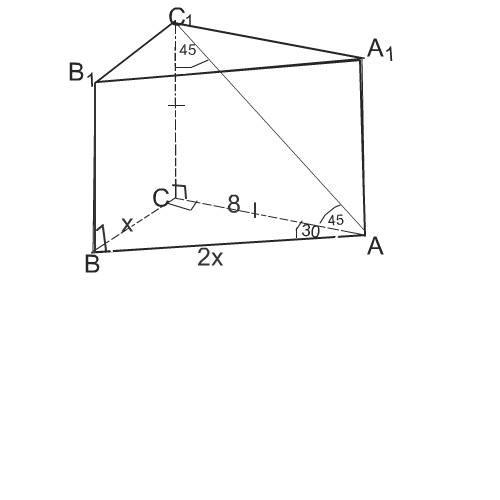
Основание призмы равно половине равностороннего треугольника, т.к. один из углов прямой, другой равен 30°, а третий, как следствие, 60°.
Следовательно, площадь двух оснований призмы равна площади полного равностороннего треугольника с высотой 8.
Площадь равностороннего треугольника, выраженная через высоту,
S=h ² : √ 3= 64 : √ 3
Площадь боковой поверхности призмы равна произведению ее высоты на периметр основания.
Высота равна 8, т.к. диагональ грани со сторонами, равными высоте и катету=8, образует со сторонами грани угол 45 градусов, и стороны грани равны.
Дальнейшие вычисления особой сложности не представляют, сумеете сделать их самостоятельно.
1. 180°-50°-70° = 60°.
ответ: 60°.
2. Треугольник прямоугольный, значит, неизвестный угол = 90°-45° = 45°.
ответ: 45°.
3. Треугольник равнобедренный, значит, углы при основании равны, неизвестные углы = 0,5(180°-80°) = 50°.
ответ: 50°, 50°.
4. Треугольник равнобедренный, неизвестный угол, вершина которого - апекс, равен 180°-15°*2 = 150°.
ответ: 150°.
5. Угол АСВ = 180°-120° = 60°. Равнобедренный треугольник с углом в 60 градусов - равносторонний треугольник. У равностороннего треугольника все углы равны по 60°.
ответ: 60°, 60°, 60°.
6. Треугольник равнобедренный, углы при основании равны, AD - биссектриса, тогда угол DAC = 50°/2 = 25°. Неизвестный угол равен 180°-50°-25° = 105°.
ответ: 105°.