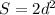Вершины треугольника АВС лежат на окружности, значит углы А, В и С - вписанные и равны половине градусной меры дуг, на которые они опираются. Угол АОС - центральный, поэтому дуга АС равна 80°. Тогда угол В, вписанный и опирающийся на дугу АС, равен 40°. <A+<C=180°-40°=140° так как сумма углов треугольника равна 180°. <A+<C=4x+3x (дано). Тогда х=140°:7=20°. <A=20*4=80°, <C=20*3=60°. Значит дуга АВ=120° (на нее опирается угол С), дуга ВС=160° (на нее опирается угол А). ответ: Дуга АВ=120°, дуга АС=80°, дуга ВС=160°.
1. 1) Пусть ABCDA1B1C1D1 - прямоугольный параллелепипед, АВ=8 м, ВС=6 м, ВВ1=2,5 м. Sбок=Pосн*h=2*(АВ+ВС)*ВВ1=2*(8+6)*2,5=2*14*2,5=70 (м²). 2) Находим количество рулонов: 70:5=14 (рулонов). ответ: 14 рулонов.
2. 1) Пусть АВСА1В1С1 - правильная треугольная призма, ВС=3 м, СВ1=5 м. Площадь полной поверхности можно найти по формуле: Sполн=Sбок+2Sосн. 2) Площадь боковой поверхности находим по формуле: Sбок=P*h=3*ВС*ВВ1. Рассмотрим ΔСВВ1 - прямоугольный, по т. Пифагора ВВ1=√(СВ1²-СВ²)=√(5²-3²)=√(25-9)=√16=4 (м). Sбок=P*h=3*ВС*ВВ1=3*3*4=9*4=36 (м²). 3) Так как основание призмы правильный треугольник, то его площадь находим по формуле: S=a²√3/4=ВС²√3/4=3²√3/4=9√3/4 (м²). 4) Sполн=Sбок+2Sосн=36+2*9√3/4=36+9√3/2=9(4+√3/2) (м²). ответ: 9(4+√3/2) м².
Пусть а - это сторона куба. Тогда площадь полной поверхности равна 6a².
Диагональ куба равна √3a, откуда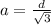 , a
, a 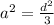
Тогда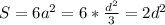
ответ: