Серединный перпендикуляр к отрезку АВ.
Объяснение:
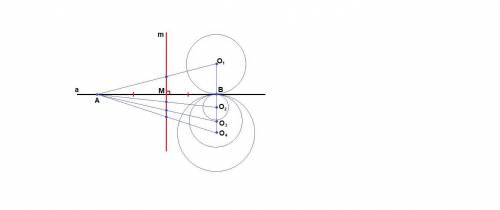
В - точка касания окружностей с прямой а, значит радиусы О₁В, О₂В, О₃В и О₄В перпендикулярны прямой а, так как радиус, проведенный в точку касания, перпендикулярен касательной.
Через точку В можно провести единственный перпендикуляр к прямой а, значит центры всех окружностей лежат на одной прямой.
Пусть прямая m - серединный перпендикуляр к отрезку АВ. Тогда m║О₁В как два перпендикуляра, проведенные к одной прямой.
По теореме Фалеса параллельные прямые отсекают на сторонах угла равные отрезки. Если точка М - середина АВ, то прямая m проходит через середины отрезков АО₁, АО₂, АО₃ и АО₄.
Значит, геометрическое место середин отрезков, соединяющих точку А с центрами окружностей, - это серединный перпендикуляр к отрезку АВ.
48 для оснований+ три грани
Объяснение:
1 полная поверхность призмы = сумма площадей всех граней
2 найдем площадь Δ или основания
S =1/2 *8 * 6= 24 (для прямоугольного треугольника формула такая же как и для прямоугольника, а*в ,только в 2 раза меньше) , так как основания два 24+24=48
3 грань призмы обычный прямоугольник - снова пригодится формула а*в. Один вопрос - Высоту знаем , а ширину нет.
4 Ширина является гипотенузой нашего треугольника, а её легко найти из т. Пифагора гипотенуза ² = катет²+ катет² = 64+36=100
⇒√100 =10
5 вернемся к шагу 3
14*10=140, это площадь одной грани , а из три
6 осталось подсчитать общую площадь
и так строим все это дело, высоты соответственно МН1,АН2,ВН3, треугольник Н3ОА подобен Н3АВ( по двум углам, так как угол АОН3=ВОН2, значит Н3АО=Н2ВО, к тому же при построении получается что АВМ равнобдренный, значит ВН3 еще и биссектриса, значит АВН3=Н3ВН2=Н3АО)
далее АН3=х, тогда ВН3= корень из 3600- х^2, раз подобны значит:
25/60=х/корень из 3600- х^2 , отсюда получаем что х=300/13
далее находим ВН3= корень из 3600- 90000/169
далее находим ОН3= корень из 625-90000/169
площадь АВМ- площадь АОМ и будет нужная площадь