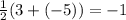Сторонами этого треугольника будут являться радиусы, следовательно треугольник равнобедренный.
Боковые углы треугольника будут равны 45 градусам. Так как треугольник равнобедренный, его высота, то есть расстояние от точки O до хорды CD, является также его медианой и биссектрисой. Поэтому треугольники, на которые делится высотой больший треугольник, являются также равнобедренными.
Следовательно, высота равна нижним катетам обоих треугольников, поэтому хорда равна высоте помноженной на два или 26 см.
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена высота. Сторона параллелограмма дана ВС=19. Необходимо найти высоту h. Вообще-то она равна 14, т.е. удвоенное расстояние от точки К до стороны АВ. Надо доказать,что расстояние от точки К до стороны ВС равно расстоянию от точки К до стороны АВ. Соединим концы биссектрис углов А и В и обозначим буквами M и N. Полученная фигура ABNM - ромб. Доказывается равнобедренность треугольников ABN и AMN через равенство противолежащих углов. Проведем перпендикуляры из точки К к сторонам ВС и AD. Они равны как высоты равных треугольников и равны расстоянию от точки К к стороне АВ, т. е. равны 7. Таким образом высота параллелограмма равна 14. Площадь равна 14*19
(-4; -1)
Объяснение:
Xb=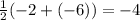
yb=