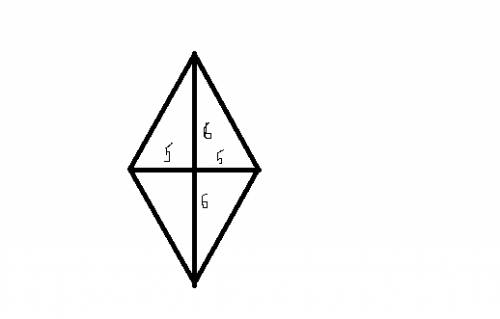
Точка пересечения O — серединная точка для обоих отрезков AD и BC.
Найди величину сторон AB и BO в треугольнике ABO, если DC = 49,2 см и CO = 49,1 см
(При ответе упорядочи вершины таким образом, чтобы углы при них были попарно равны.)
А. Так как отрезки делятся пополам, то
1. сторона BO в треугольнике ABO равна стороне в треугольнике DCO;
2. сторона AO в треугольнике ABO равна стороне в треугольнике DCO.
Угoл BOA равен углу как вертикальный угол.
Треугольники равны по первому признаку равенства треугольников.
В равных треугольниках соответствующие стороны равны.
AB =
см;
BO =
см.
ответ:
объяснение:
1) 2*9=18- это две стороны по 9, 26-18=8/2=4-это другая сторона, s=9*4=36
2)s=a*a=169, a=13, p=13*4=52
3) s=a*b=96, 3*b=96, b=96/3=32, p=2(a+b)=2(3+32)=70
4)4a=164, a=164/4=41
6)a=x, b=6x, 2(x+6x)=70, 7x=35, x=5, 6x=6*5=30, a=5, b=30, s(пр)=5*30=150, s(кв)=150, (у равновеликих фигур площади равны),
s(кв)=a^2, a^2=150, a=v150=v(25*6)=5v6, p(кв)=4*5v6=20v6
7)s=a^2*v3/4=36*v3/4=9v3