Объяснение:
Периметр треугольника - сумма длин всех сторон.
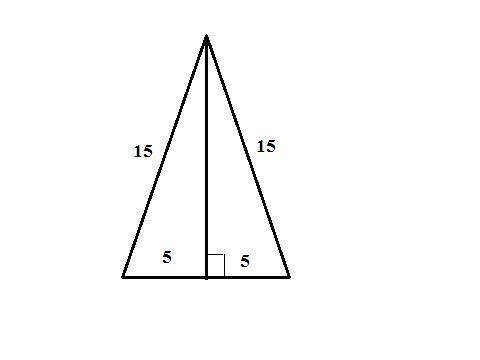
Данный треугольник равнобедренный.
Основание 10 см, боковые стороны по 15 см.
Р=10+15*2=40 см.
Площадь треугольника - S=ah/2, где a - сторона треугольника, h - васота проведенная к ней.
Из вершины равнобедренного треугольника проведем высоту к основанию. По свойству высоты проведенной из вершины она является так-же и медианой. Следовательно высота, половина основания и боковая сторона образуют прямоугольный треугольник, где катет (высота) находится по т. Пифагора - √(15²-5²)=10√2 см.
Тогда площадь треугольника - 10*10√2/2=50√2 см².
∠AKB = ∠DBC; это - внутренние накрест лежащие углы; а
∠DBC = ∠ABD; так как BD - биссектриса
получилось, что треугольник AKB - равнобедренный.
Теперь понятно, что для того, чтобы прямая AD пересекла BС в точке C за точкой D, то есть чтобы существовал треугольник ABC, нужно, чтобы точка D лежала ближе к B, чем K.
Отсюда ∠ADB > ∠AKB = ∠ABD; и AB > AD; так как напротив большего угла в треугольнике лежит большая сторона.