сделаем построение по условию
сторона квадрата b= 4см
диаметр окружности d=b=4см
радиус окружности r=d/2=4/2=2 см
периметр состоит
из двух сторон квадрата 2*b=2*4=8
и
из двух полуокружностей L/2 с радиусом r=2 см
две полуокружности - это полная окружность
длина окружности L=2п*r
Периметр Р=2*b+2*L/2=2b+L=2*4+2п*r=8+2*п*2=8+4*3.14=20,56 см
площадь состоит
из площади квадрата Sкв=b^2
и
из площадей двух полукругов Sкр / 2 = п*r^2 / 2
площадь S=Sкв + 2*Sкр / 2 =Sкв + Sкр = b^2 +п*r^2 = 4^2 + п*2^2 = 16+3.14*4 =28,56 см2
ОТВЕТ
площадь 28,56 см2
Периметр 20,56 см
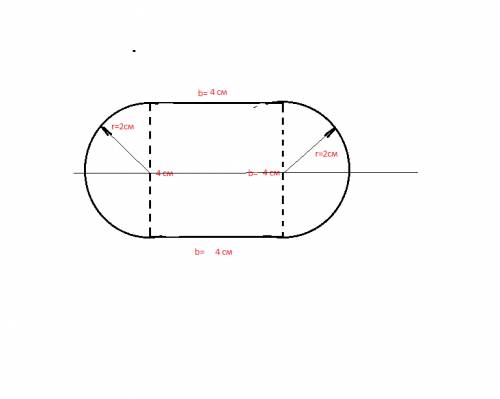
сделаем построение по условию
сторона квадрата b= 4см
диаметр окружности d=b=4см
радиус окружности r=d/2=4/2=2 см
периметр состоит
из двух сторон квадрата 2*b=2*4=8
и
из двух полуокружностей L/2 с радиусом r=2 см
две полуокружности - это полная окружность
длина окружности L=2п*r
Периметр Р=2*b+2*L/2=2b+L=2*4+2п*r=8+2*п*2=8+4*3.14=20,56 см
площадь состоит
из площади квадрата Sкв=b^2
и
из площадей двух полукругов Sкр / 2 = п*r^2 / 2
площадь S=Sкв + 2*Sкр / 2 =Sкв + Sкр = b^2 +п*r^2 = 4^2 + п*2^2 = 16+3.14*4 =28,56 см2
ОТВЕТ
площадь 28,56 см2
Периметр 20,56 см

Точка О делит диагонали пополам, тогда AO=CO=6, BO=DO=10. Из треугольника BOA можно найти AB по теореме косинусов: AB^2=BO^2+OA^2-2*BO*OA*cosBOA=100+36-2*10*6*1/2, AB=sqrt(76)=2sqrt(19). Из треугольникаа BOC надйем BC, зная, что угол BOC равен 120, а его косинус равен -1/2: BC^2=BO^2+CO^2-2*BO*CO*(-1/2)=100+36+60=196, BC=14. В параллелограмме противоположные стороны равны, тогда CD=2sqrt(19), AD=14.