1. Можно описать окружность около любого треугольника.
2. Около квадрата можно описать окружность.
3. Около прямоугольника можно описать окружность, центр ее совпадает с точкой пересечения диагоналей. Вписать окружность в прямоугольник нельзя
4.Около прямоугольника можно описать окружность.
5. Окружность можно описать вокруг ромба, только если он квадрат.
Я так полагаю, что верны утверждения 1,3,4..Описывать фигуры около окружности вообще не принято. Только если вписывать фигуры в окружность.
Эти задачи не покажутся сложными, если научишься пользоваться интернетом, когда что-то из пройденного материала забыла. Все формулы и объяснения там есть.
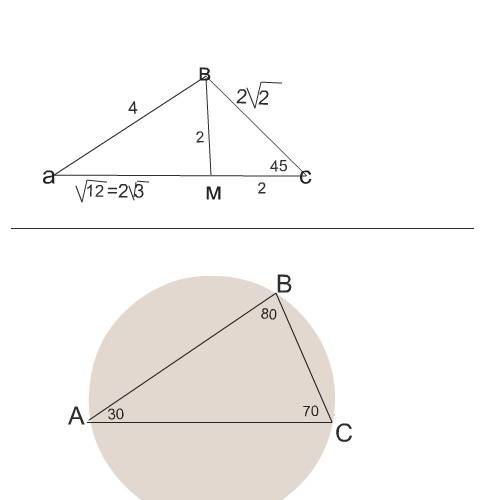
задача1. Рисуешь треугольник. Две стороны в нем известны, известен и один угол=45°.
Проводишь высоту вм к основанию. Получаешь равнобедренный треугольник всм, так как один угол прямой при основании высоты, второй дан 45°, третий тоже будет 45°. По теореме Пифагора или просто потому что помнишь, что вс=2√2 здесь равна диагонали квадрата, находишь вм=мс=2.
Теперь из прямоугольного треугольника авм находишь ам по теореме Пифагора. Можно обратить внимание, что этот треугольник - половина равностороннего, так как вм=половине ав.
В любом случае ам=2√3
ас=2√3+2=2(√3+1)
_____________________________________________
задача 2.
третий угол А в этом треугольника равен 180-80-70=30°
Одна из формул радиуса описанной окружности
R = a:(2·sin A).
а- это сторона против угла А.
а=8, угол А=30° и его синус 1/2.
R = a:(2·sin A)=8:(2·1/2)= 8 см
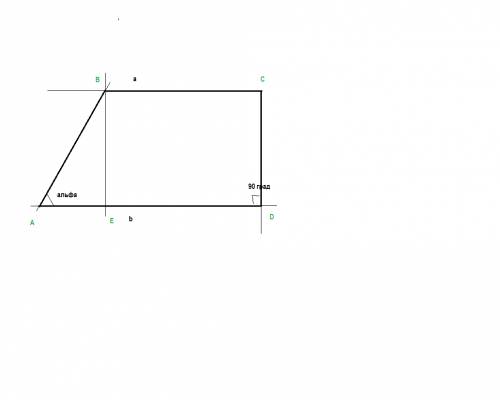
на рисунке сделаем построение по условию
ВС=а
AD=b
трапеция прямоугольная
значит
<C=<D=90 град
<A= альфа <B=180 - альфа
опустим перпендикуляр ВЕ из вершины В на сторону AD
получился прямоугольный треугольник АВЕ , где <BEA =90 Град
сторона AE=AD-BC=b-a
a)если а = 4 см, b= 7 см, альфа = 60° НАЙТИ : AB -большая боковая сторона
сторона АВ=АЕ/cos(альфа)=(b-a)/cos(альфа)=(7-4)/cos60=3/(1/2)= 6 см
б)если альфа=10 см,b=15 см, альфа=45° НАЙТИ CD - меньшая боковая сторона
сторона ВЕ=АЕ/sin(альфа)=(b-a)/sin(альфа)=(7-4)/sin45=3/(1/√2)=3√2 см
ответ а) 6 см б) 3√2 см
3,4,5
Объяснение:
окружность можно описать около любого треугольника и четырехугольника, у которого суммы противоположных углов равны 180 градусам (под это утверждение подходит 4 вариант)
около окружности можно описать любой треугольник и четырехугольник, суммы противоположных сторон которого равны (под это утверждение подходят 3,5 варианты)