Дано :
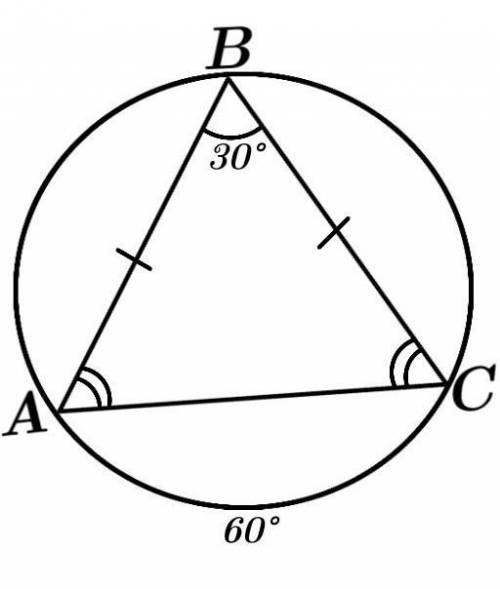
∆АВС — равнобедренный, вписан в окружность.
АС — основание = радиус описанной окружности.
Найти :
∪АС = ?
∪АВ = ?
∪ВС = ?
Если хорда равна радиусу окружности, то она стягивает дугу в 60°.АС — хорда описанной окружности, поэтому ∪АС = 60° (по выше сказанному).
∠АВС — вписанный (по определению).
По свойству вписанных углов —
∠АВС = 0,5*∪АС
∠АВС = 0,5*60°
∠АВС = 30°.
Углы у основания равнобедренного треугольника равны.Поэтому, по теореме о сумме углов треугольника —
∠АСВ = ∠ВАС = 0,5*(180° - ∠АВС) = 0,5*(180° - 30°) = 0,5*150° = 75°.
Причём ∠АСВ и ∠ВАС — вписанные по определению.
Равные вписанные углы опираются на равные дуги.Тогда —
∪АВ = ∪ВС = 2*∠ВАС = 2*75° = 150°.
60°, 150°, 150°.
Требуется по известному объёму шара, равного 36 * π см3, определить площадь поверхности сферы, которая ограничивает этот шар.
Как известно, объём шара (V) при известном радиусе R, вычисляется по формуле V = (4/3) * π * R3.
Согласно условия задания, имеем, (4/3) * π * R3 = 36 * π см3, откуда R3 = (36 * π см3) : ((4/3) * π) = 27 см3.
Последнее равенство позволяет определить длину радиуса шара (что тоже самое, длину радиуса сферы, которая ограничивает шар): R = 3 см.
Теперь легко вычислить площадь (S) поверхности сферы по формуле: S = 4 * π * R2 .
Имеем: S = 4 * π * R2 = 4 * π * (3 см)2 = 4 * π * 9 см2 = 36 * π см2 .
ответ: 36 * π см2.
ответ: найдем проекцию отрезка A1C на плоскость A1B1C1. Этой проекцией будет отрезок A1C1. A1C1 перпендикулярен к отрезку B1D1, т.к. диагонали в квадрате пересекаются под прямым углом. Проведем в плоскости A1B1C1 через точку A1 прямую, параллельную отрезку B1D1, которую назовем L. По теореме о трёх перпендикулярах т.к. L перпендикулярна проекции наклонной, то L перпендикулярна и самой наклонной A1C. А т.к. L и B1D1 параллельны, то и B1D1 перпендикулярен к A1C.
Объяснение: