+2 задание:
Рассмотрим треугольник DME:
предположим ,что угол DME - тупой (будет смежным с острым углом этого треугольника) и угол DEM - острый (так как двух углов тупых не может быть в треугольнике по определению и признаку треугольника) .
Если напротив большего угла в данном треугольнике лежит самая большая сторона,то DE>DM.
Что и требовалось доказать.
+3 задание:
уголN=180-(69+37)=74
уголMNP=74/2=37
угол NPM=180-(37+69)=74
уголNPK=180-(37+37)=69
угол MPN=74
уголNPK=69
уголMPN больше угла NPK, то MPменшеРК
+4 задание:
С=180-76-66=38
ЕК - биссектриса => КЕС=38
С=КЕС => треугольник КЕС равнобедренный, КС=ЕК
В треугольнике против большего угла лежит большая сторона
DEK<D => DK<EK=КС DK<КС
Здравствуйте, Jdirjmnab!
Решим данную задачу алгебраическим через уравнение).
Формула периметра тр-ка: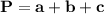
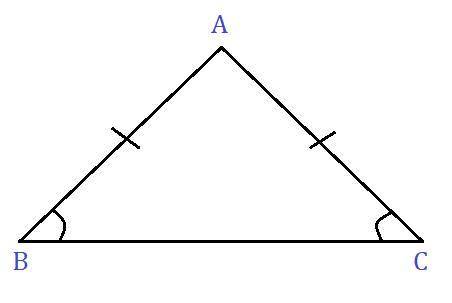
Пусть x (см) равна боковая сторона, тогда основание будет равно (x-14) (см). Т.к. боковые стороны равнобедренного тр-ка равны, то вторая боковая сторона тоже x (см). Периметр тр-ка равен 76 (см).
I этап. Составление математической модели:
II этап. Работа с математической моделью:
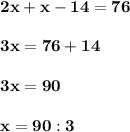
III этап. ответ математической модели:
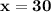(см) равна боковая сторона.
IV этап. ответ на вопрос задачи:
Т.к. боковые стороны равны, то их сумма равна 30+30=60 (см).
Тогда основание равно: 76-60=16 (см) или 30-14=16 (см).
Проверка:По правилу сумма двух сторон тр-ка должна быть больше одной стороны.
30+30>16 - верно; 30+16>30 - верно; 30+16>30 - верно.
Окончательный ответ задачи:В данном тр-ке: "боковые стороны по 30 (см), основание 16 (см).
С Уважением, NeNs07.
сли один угол больше другого на 50° и такие углы образованы при пересечении параллельных прямых секущей, то они или смежные, или внутренние односторонние, т.к в ином случае (если они накрестлежащие, вертикальные) они бы были равны.
Сумма смежные углов или внутренних односторонних, образованных при пересечении секущей параллельных, всегда равна 180.
Пусть один -х, тогда другой х+50
х+(х+50)=180
2х=180-50
2х=130
х=130:2
х= 65°- один угол;
65+50=115°
Объяснение: