а) Доказано; б) 36
Объяснение:
а)
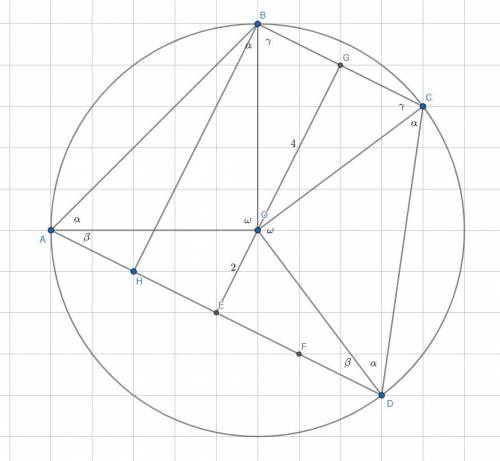
Обратимся к первому рисунку. Пусть ∠AOB=∠COD=ω. Тогда ∠BAO=∠ABO=∠OCD=∠ODC=α (AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а =>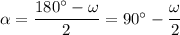 
). ΔAOD равнобедренный (AO=OD=R) => ∠OAD=∠ODA=β. Аналогично ∠OBC=∠OCB=γ. Т.к. четырехугольник вписан в окружность, то ∠BAD+∠BCD=180°. Значит: 
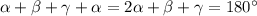. ∠BAD+∠ABC=
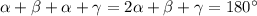. Получили, что 
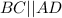, т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.
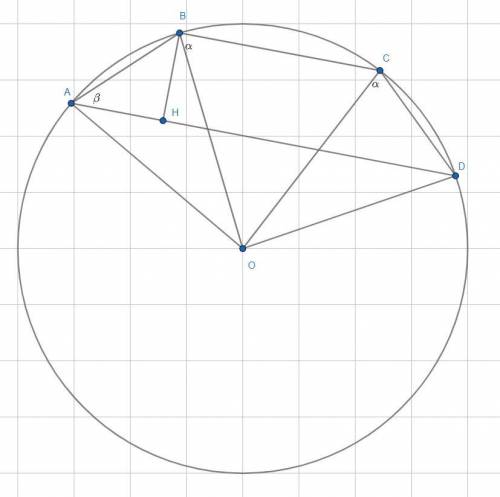
Заметим, что центр описанной около четырехугольника окружности может лежать вне него. Тогда доказательство будет отличаться. Начиная с этого момента забудем о тех обозначениях, которые были введены для доказательства первого случая. Обратимся ко второму рисунку. Заметим, что ∠ABC=∠BCD=α, так как AO=OB=R и CO=OD=R => треугольники ABO и COD равнобедренные, в которых угол против основания общий, а =>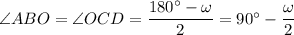 
(здесь ∠AOB=∠COD=ω) и ∠OBC=∠BCO, так как это углы при основании равнобедренного треугольника BOC (OB=OC=R). Пусть ∠BAD=β. Тогда 
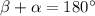(так как четырехугольник вписанный). Но 
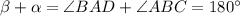. Значит 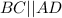, т.к. внутренние односторонние углы при этих прямых и секущей AB в сумме дают 180°. Поскольку AD≠BC (по условию AD=2BC), четырехугольник трапеция, а не параллелограмм, а так как она вписана в окружность, то равнобедренная. Доказано.
б)
Решим задачу для 1-ого случая:
Пусть EG - расстояние между прямыми BC и AD. Т.к. BC||AD, то EG=6. Заметим, что треугольники BOC и AOD равновеликие.
Докажем это:
Пусть ∠BOC=α. Тогда (так как ∠AOB=∠COD=90°, а => ∠BOC+∠AOD=360°-90°-90°=180°) ∠AOD=180°-α.
Получим:
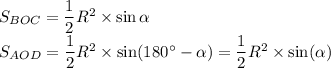
Запишем их площади через формулу про основание и высоту:
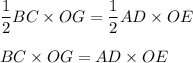
Из условия следует, что AD=2BC.
Тогда:
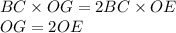
Знаем, что:
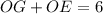
Тогда:
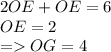
Поскольку треугольники BOC и AOD равнобедренные, то OG и OE не только их высоты, но и медианы соответственно, а значит BG=BC/2 и AE=AD/2.
Тогда из прямоугольных треугольников BOG и AOE по теореме Пифагора найдем BC и AD:
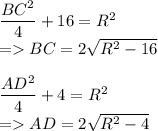
По условию AD=2BC.
Значит:
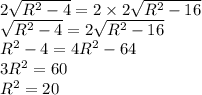
Теперь находим BC и AD:
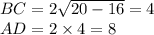
Теперь можно без труда найти площадь трапеции:
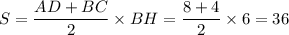
Получили, что площадь трапеции ABCD равна 36.
Задача решена!
(Для второго случая решить пункт б) невозможно, так как дуга AB + дуга CD по условию должны давать 180°, что невозможно для данного случая)
Сначала Чингисхан одержал победу в междоусобных войнах в Монголии, а, начиная, с 1202 года, встал во главе завоевательных походов.В 1202 году Темучином с особой жестокостью были сокрушены татарские войска. В 1204 году в борьбе за власть в Монголии Чингисхан сокрушил могущественного хана Джамуху – человека, с которым они дружили в детстве и шли в бой плечом к плечу в своих первых сражениях.Официально прозвище «Чингиз хан», т.е. «повелитель воды» Темучин получил в 1206 году, когда Курултай (большое собрание) избрал его ханом. Чингисхан провёл ряд административных реформ в родной стране, но он хотел власти над большей частью мира.В 1207-1211 году войска Темучина, во главе которых стоял он сам и его сыновья, совершили наступательный поход на Северный Китай. Монголы завоевали часть империи Цзинь в районе Великой Китайской стены и почти дошли до Пекина.Пекин был взят монгольскими войсками в 1215 году, в городе полыхали пожары, вся местность вокруг была превращена в пустыню.После завоевания Китая Чингисхан начал сбор войск для завоевания преуспевающей и цветущей Средней Азии. Этот поход начался в 1218 году и был ознаменован рядом громких завоеваний. Монголы взяли Бухару, Самарканд, Ургенч – древние среднеазиатские центры.В 1220 году пал Северный Иран, монголы пришли и в Крым.Первое столкновение страшных кочевых племён с европейцами произошло в 1223 году. Это была печально знаменитая в русской истории битва на реке Калке. В этом сражении монголы нанесли тяжёлое поражение русско-половецким войскам, в нём погибли знаменитые русские князья. Битва на Калке стала предвестником будущего завоевательного похода монголов на Русь.
Объяснение:
если не правильно извени ಥ‿ಥ