Дано:
△ABC - равнобедренный.
AC - основание.
AH и CN - высоты.
∠HON = 140˚
Найти:
∠CBO.
Решение.
Рассмотрим △BHO и △BNO:
Они прямоугольные.
BO - общая сторона.
BN = BH, т.к. △ABC - равнобедренный.
=> △BNO = △BHO, по гипотенузе и катету.
Т.к. △BNO = △BHO => ∠HOB = ∠NOB = 140 : 2 = 70˚
СУММА ОСТРЫХ углов прямоугольного треугольника равняется 90°
=> CBO = 90 - 70 = 20˚
ответ: 20°.

Сторони паралелограма будуть 10см; 10см; 12см; 12см;
Объяснение:
Щоб найти площу паралелограма потрібно сторону помножити на висоту, тобто S=ah, а нам відомо, що висота у 4 рази менша, значить сторона на яку вона спираєть буде у 4 рази більша і в нас є площа і можна найти висоту і тут буде рівняння ( відчуваю себе розумною). 36=4х * х; 36=4х2; 9=х2; 3=х - ми найшли висоту.
Тоді сторона буде 3*4=12 а протилежні сторони рівні
тоді від периметра віднімаємо дві сторони 44-12-12=20 знайшли дві ще сторони і ділемо на два
20:2=10
Все
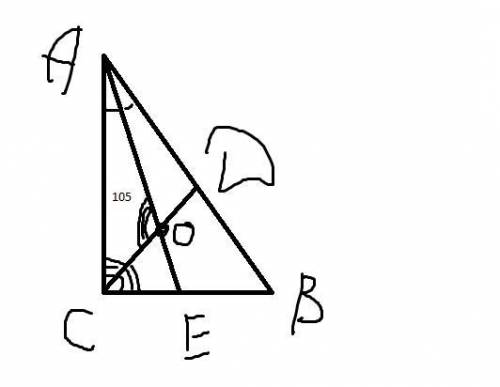
∠B = 30°
Пояснение:
Дано: Δ АВС, ∠С = 90°, ∠АОС = 105°, биссектрисы CD и АЕ, что пересекаются в точке О
Найти: меньший острый угол Δ АВС
Решение
∠CAO = ∠OAD (так как биссетриса AE делит угол ∠А пополам)
∠ACD = ∠OCB= ∠C/2 = 90°/2 = 45° (так как биссетриса CD делит угол ∠C пополам)
Рассмотрим Δ CAO, в котором ∠CAO = 45°, ∠АОС = 105°, ∠CAO - ?
Так как сумма всех углов в треугольнике равна 180°, то
∠CAO = 180° - (105° + 45°) = 180° - 150° = 30°
∠CAO = ∠OAD = 30°, следовательно ∠А = ∠CAO + ∠OAD = 60°
Рассмотрим Δ АВС, в котором ∠С = 90°, ∠А= 60, ∠B - ?
Так как сумма углов при катетах в прямоугольном треугольнике равна 90°, то
∠B = 90° - ∠А = 90° - 60° = 30°
ответ: ∠B = 30°
20
Объяснение:
ВВ1- высота, но тк ∆равнобедренный он является ещё и биссектрисой.
из четырёхугольника ОNBH найдём угол <NBH=360°-90°-90°-140°=40°
И тк ВВ1 биссектриса, <CBO=40°:2=20°