Начертите равносторонний треугольник со стороной 4см. Проведите в нем биссектрисы углов и впишите в этот треугольник окружность. Вычислите и измерьте радиус этой окружности.

👇

Открыть все ответы

Ответ:

noellajyli

30.09.2022

Окружность описана, значит суммы ее противоположных сторон равны. Т.е. сумма боковых сторон равна сумме оснований. Так как трапеция равнобедренная то боковые стороны равны. Значит сумма боковых сторон равна сумме оснований равна 5+5=10 см.

Так как угол равен 30. То катет лежащий против нее равен половине гипотенузы, катетом будет высота трапеции, а гипотенузой боковая сторона. Значит высот равна 5:2=2,5 см.

Площадь трапеции равна произведению половине суммы оснований на высоту, значит: 10:5*2,5=12,5 кв.см

Объяснение:

4,7(88 оценок)

Ответ:

R5R5ty

30.09.2022

Дано:

Правильная четырёхугольная пирамида SABCD;

Сторона основания AD = ;

Боковое ребро SD = .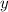

Найти:

V = ?

Решение: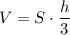

$V=S\cdot\dfrac{h}{3}$

Поскольку в основании правильной четырёхугольной пирамиды лежит квадрат, то S основания = Ѕ квадрата = 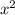x^2

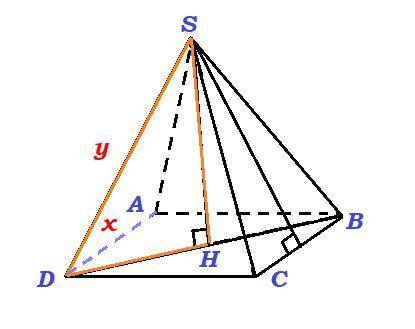
Вершина высоты правильной пирамиды проецируется в центр ее основания - здесь это точка пересечения диагоналей квадрата.

Высоту h пирамиды найдём из прямоугольного треугольника SHD, гипотенуза которого равна боковому ребру пирамиды, a катет DH равен половине диагонали основания.

Диагонали квадрата равны.

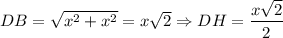
⇒ $DB =\sqrt{x^2+x^2} =x\sqrt{2} \Rightarrow DH=\dfrac{x\sqrt{2}}{2}$

Найдём 2 катет по т.Пифагора (он же высота пирамиды):

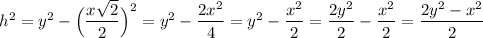
$h^2=y^2-\Big(\dfrac{x\sqrt{2}}{2}\Big)^2=y^2-\dfrac{2x^2}{4}=y^2-\dfrac{x^2}{2}=\dfrac{2y^2}{2}-\dfrac{x^2}{2}=\dfrac{2y^2-x^2}{2}$

Отсюда: 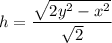$h=\dfrac{\sqrt{2y^2-x^2}}{\sqrt{2}}$ .

Остаётся найти ответ на вопрос: чему равен объём пирамиды.

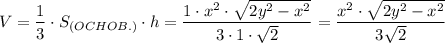$V =\dfrac{1}{3}\cdot {S}_{(OCHOB.)} \cdot h=\dfrac{1\cdot x^2\cdot\sqrt{2y^2-x^2}}{3\cdot1\cdot\sqrt{2}}=\dfrac{x^2\cdot\sqrt{2y^2-x^2}}{3\sqrt{2}}$ .

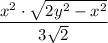
ответ: $\dfrac{x^2\cdot\sqrt{2y^2-x^2}}{3\sqrt{2}}$
Дана правильная четырехугольная пирамида. Стороны основания равны х, а боковое ребро у. ВЫчислить об