Объяснение:
1. Только на рис. Б сумма внутренних односторонних углов равна
43 + 137 = 180°. ⇒ На рис Б прямые параллельны по признаку параллельности прямых
2. По теореме о внешнем угле треугольника, внешний угол равен сумме двух других углов, не смежных с ним. Зная это, можем составить уравнение:
110 = 6х+24 + 3х + 10.
Решим его:
110 = 9х + 34
76 = 9х
х = 76/9
∠С = 76/9 *6 + 24 = 152/3+24 = 50 целых и 2/3 + 24 = 74 целых и 2/3
3. В прямоугольном треугольнике второй угол = 180 - 90 -60 = 30°
По свойству прямоугольного треугольника катет, лежащий против угла 30° равен половине гипотенузы. При чем, этот катет и будет меньшим, как лежащий напротив меньшего угла. Пусть искомый катет будет х, тогда гипотенуза = 2х. Составим уравнение:
х + 2х = 27,9
3х = 27,9
х = 9,3. Гипотенуза = 18,6
4. В Δ АВС ∠B = 180- 110 - 15 = 55°
В Δ ВСС₁ ∠ С = 55°, как половина угла ВСА. ⇒ Δ ВСС₁ равнобедренный, BC₁ = CC1 = 12 см
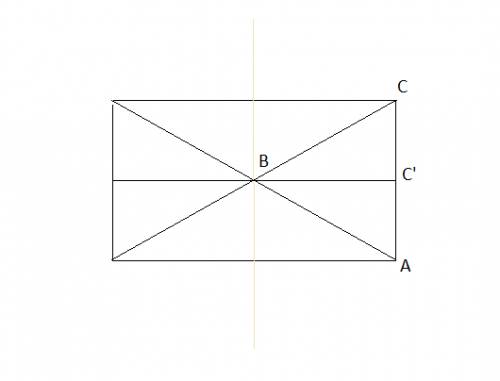
ABC - равнобедренный треугольник, AC = 8, P_ABC = 18, V_тела вращения = V_цилиндра с высотой равной основанию треугольника и радиусом равным высоте треугольника - 2*V_конуса с радиусом основания равным высоте треугольника и высотой равным половине основания треугольника
V_цилиндра = pi*r^2*h
Радиус найдём воспользовавшись теоремой Пифагора и тем, что наш треугольник равнобедренный. AB = BC = (P_ABC - AC)/2 = (18-8)/2 = 5, r_основания цилиндра (=высоте треугольника) = V(AB^2+(AC/2)^2) = V25 + 16 = V41 (Корень), (высоту искали из прямоугольного треугольника ABC', C' делит AC пополам)
V_цилиндра = pi*r^2*h= pi * 41 * 8 =328pi
V_конуса = 1/3*pi*(r_конуса)^2*h_конуса = 1/3*pi*41*4 =123/3*pi
V_тела вращения = V_цилиндра - 2*V_конуса = 328pi - 246/3*pi = (328-82)pi = 246pi
Мк отрезок
РМ =22.6
КР =15.7
КМ-?
Объяснение:
КМ=РМ-КР
КМ =22.6-15.7
КМ=6.9
ответ :КМ =6.9