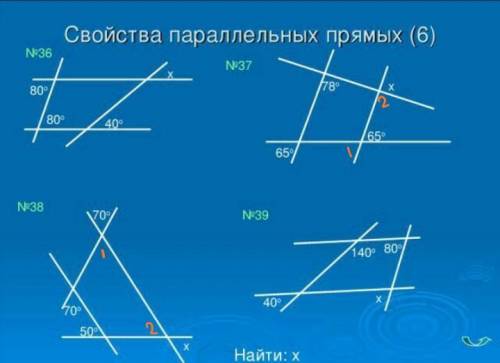
37. Решение:
∠1=65° (как вертикальные)
∠1 и угол в 65° равны, как соответственные углы при пересечении двух прямых секущей. Отсюда прямые параллельны. Значит ∠2=78° (как соответственные)
Поскольку сумма смежных углов равна 180°, то
х=180°-∠2=180°-78°=102°
ответ: 102°
38. Решение (аналогично):
∠1=70° (как вертикальные)
∠1 и угол в 70° равны, как соответственные углы при пересечении двух прямых секущей. Отсюда прямые параллельны. Значит ∠2=50° (как соответственные)
х=∠2 (как вертикальные)
х=50°
ответ: 50°
(Чертёж в приложении)
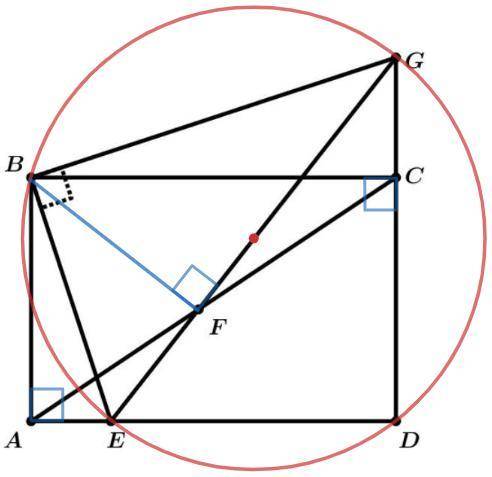
Точки A-F-C лежат на прямой Симсона точки B относительно треугольника EGD.
Объяснение:
Основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на прямой Симсона.
Точка B лежит на описанной окружности треугольника EGD (прямые углы EBG и EDG опираются на диаметр EG).
A и С - основания перпендикуляров из точки B на стороны треугольника EGD.
Тогда AC - прямая Симсона точки B относительно треугольника EGD.
(Прямая Симсона пересекает сторону EG в точке F, следовательно BF⊥EG)
а) Прямая AD перпендикулярна плоскости SCD т.к. она перпендикулярна двум пересекающимся прямым этой плоскости (SD т.к. ABCD - прямоугольник, и SD по условию) Значит AD перпендикулярна любой прямой плоскости SCD в том числе и SC
б) Опустим перпендикуляр из В на плоскость АСМ в точку Н и перпендикуляр на прямую АС в точку Е. Тогда ВЕ как высота из прямого угла равна АВ * ВС / АC = 8 * 6 / 10 = 4.8 (АС по теореме Пифагора 10)
По условию синус НЕВ равен 5/6 т.е. BH = BE*5/6 = 4.8*5/6 = 4