1. а) 176 см²; б) 4 см.
2. 113,4 см²
3. 7,8 см.
4. 1) 5 см; 2) 10 см; 3) 8 см.
Объяснение:
1. Площадь параллелограмма равна S=ah.
a) S=16*11=176 см ².
б) S=ah; a=S/h=102/25.5=4 см .
***
2. Проведем высоту ВЕ⊥AD.
Из ΔАВЕ ВЕ/АВ=Sin30°, откуда ВЕ=14*(1/2)=7 см.
S=AD*BE=16.2*7= 113.4 см².
***
3. S=ah, где а=9 см, b =2.6 см; S=9*2.6= 23.4 см².
S=ah, где а=3. Найдем h.
3h=23.4;
h=23.4/3;
h=7.8 см.
Доп. вопрос: Не зависит, главное, чтобы она была правильной и применима к данной фигуре.
***
4. 2h=a;
S=ah;
H=2(a+b).
S=2h*h=50;
2h²=50;
h²=25;
h=√25=±5; (-5 - не соответствует условию).
1) h=5 см .
а=2h=2*5=10 см.
2) а=10 см.
Р= 2(a+b);
2(10+b)=36;
10+b=18;
3) b=8 см.
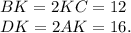
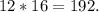

Привет, вот решение
Построить угол, равный:
а) 30°: б) 60°; в) 15°; г) 120°; д) 150°; е) 135°; ж) 165°; з) 75°; и) 105°
а) План построения:
1) строим произвольную прямую а и произвольную точку А на прямой а,
2) строим прямую b что
3) строим точку В, что ∆АВС - прямоугольный (по построению) и (по построению), значит (т.к. катет противолежащий этому углу равен половине гипотенузы).
б) получаем
(т.к. ∆АОВ - прямоугольный и )
в) делим пополам, получаем 15°.
г) т.к. 120°=180о-60°, то этот угол построен в п.а) - это угол, смежный
д) т.к. 150°= 180°-30°, то этот угол построен в п.а) - это угол смежный
е) т.к. 135°=90°+45°, то строим две перпендикулярные прямые и один из полученных прямых углов делим пополам;
ж) т.к. 165°= 180°-15°, то это угол, смежный построенному в п.в), т.е. углу в 15°.
з) т.к. 75°=90°-15°, то строим угол в 15°, потом строим перпендикуляр к одной из сторон построенного угла, проходящий через его вершину. Один из полученных углов будет 75°.
и) т.к. 105°=90о+15°, то это другой из углов, полученных в пункте