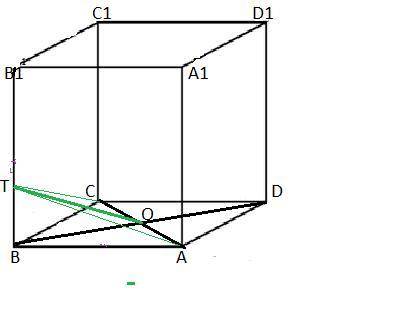
В кубе ABCDA1B1C1D1, ребра которого равны 4, на ребре BB1 взята точка T так, что BT:TB1=1:3. Найти синус угла между плоскостями (АВС) и (АТС)
Объяснение:
Т.к. BT:TB₁=1:3 и ВВ₁=4 ,то ВТ=4:4*1=1 (см).
Из ΔАВС-прямоугольного , по т. Пифагора найдем
АС=√(4²+4²)=4√2 (см). Значит ВD=4√2 см⇒ВО=2√2 см.
В кубе все грани квадраты⇒АС⊥ВD и ТВ⊥ВD ⇒ по т. о трех перпендикулярах ∠ТОВ-линейный угол между плоскостями (АВС) и (АТС).
ΔВТО-прямоугольный , по т. Пифагора ТО²=ВТ²+ТО². ТО=3 см.
sin∠ТВО=ТВ/ТО, sin∠ТВО=1*3.
Синус угла между плоскостями (АВС) и (АТС) равен 1/3.
Якщо ще актуально)
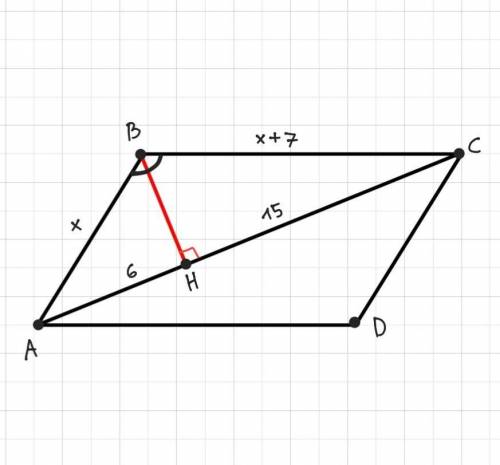
Дано: ABCD - паралелограм, АС - діагональ, ВН⟂АС, АН= 6 см, СН= 15 см, ВС–АВ= 7 см.
Знайти: S abcd.
Розв'язання.
Розглянемо трикутники АНВ і СНВ.
Вони прямокутні, а сторона ВН для них є спільним катетом. АН= 6 см, СН= 15 см, тому очевидно, що ВС>АВ.
Нехай АВ= х см, тоді ВС= (х+7) см.
Оскільки ВН - спільна сторона, тоді справедлива така рівність (через т.Піфагора у ΔAHB і ΔCHB):
АВ²–АН²= ВС²–НС²;
х²–6²= (х+7)²–15²;
х²–6²= х²+14х+49–225;
х²–х²–14х= 36+49–225;
–14х= –140;
14х= 140;
х= 10 (см)
Отже, АВ= 10 см, тоді:
ВН²= х²–6²= 10²–6²= 100–36= 64;
ВН= 8 см (–8 не може бути)
Розглянемо ΔABC:
AC= AH+HC= 6+15= 21 см
ВН= 8 см, ВН - висота ΔABC, оскільки ВН⟂АС.
Знайдемо площу ΔАВС:
S= ½•AC•BH;
S= ½•21•8= 84 (см²).
Діагоналі паралелограма ділять його на два рівних трикутники, тобто їх площі рівні.
SΔABC= SΔCDA= 84 см²
Звідси площа паралелограма ABCD дорівнює
S abcd= 2•SΔABC= 2•84= 168 (см²).
Відповідь: 168 см².
35см²