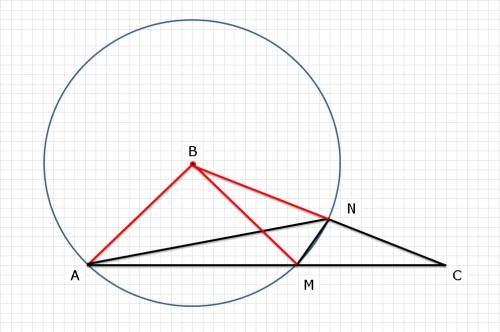
У каждого из треугольников ABM, ABN, MBN две стороны – это радиусы окружности. Значит, все эти треугольники равнобедренные.
Решаем:
< ABC = 180⁰ - (<BAC + <BCA) = 180⁰ - (32⁰+24⁰) = 124⁰
< BMA = <BAM = 32⁰
< ABM = 180⁰ - (<BMA + <BAM) = 180⁰ - (32⁰+32⁰) = 116⁰
< MBN = <ABC - <ABM = 124⁰ - 116⁰ = 8⁰
< BNM = <BMN = (180⁰ - 8⁰)/2 = 86⁰
< BNA = <BAN = (180⁰ - 124⁰)/2 = 28⁰
< ANM = <BNM - <BNA = 86⁰ - 28⁰ = 58⁰
ответ: < ANM = 58⁰
Объяснение:
ответ, проверенный экспертом
4,6/5
237
Владимир1111111
хорошист
12 ответов
3.4 тыс. пользователей, получивших
Пусть х- один угол, тогда второй - х+30. При пересечении диагоналей образуется прямоугольный треугольник с углом 90 градусом.
х+х+30+90=180
2х+120=180
2х=60
х=30
1 угол = 30 градусов, тогда 2 угол 2х30=60
Поскольку ромб это параллелограмм то он имеет все свойства параллелограмма, соответственно противолежащие углы равны. Тоесть, если 1 угол равен 30, то противолежащий угол тоже равен 30 градусов. С 2 углом тоже самое. ответ: 30, 60, 30, 60.
Такс, в ромбе диагональ выполняет функцию биссектрисы, значит 2х30=60, 2х60=120, потому что биссектриса делит углы пополам.