Question

С геометрией Задание на фото.

Answer 1

Пусть AC=x, тогда в ΔABC по формуле Герона:

$\displaystyle 4S=\sqrt{(17+39+x)(17+39-x)(17-39+x)(39-17+x)}\\\\4\cdot 330=\sqrt{(56^2-x^2)(x^2-22^2)}\\\\x^4-(56^2+22^2)x^2+4^2\cdot 330^2+56^2\cdot 22^2=0$

Решим квадратное уравнение относительно x².

$\displaystyle x^2=\frac{+(56^2+22^2)\pm \sqrt{(56^2+22^2)^2-4\cdot 88^2\cdot (14^2+15^2)}}{2}$

Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:

$\begin{bmatrix}x=\sqrt{\dfrac{56^2+22^2+252}2}\\\\x=\sqrt{\dfrac{56^2+22^2-252}2}\end{matrix} \;\begin{bmatrix}x=44\qquad \\x=2\sqrt{421}\end{matrix}$

Пусть KL=a, KN=b.

Рассмотрим случай, когда AC=44.

В ΔABC по теореме косинусов:

$\displaystyle \cos A=\frac{44^2+17^2-39^2}{2\cdot 44\cdot 17} =\frac8{17}$

$\displaystyle \cos C=\frac{44^2+39^2-17^2}{2\cdot 44\cdot 39} =\frac{12}{13}$

По формуле связи косинуса и тангенса:

$\displaystyle tgA=\sqrt{\frac{17^2-8^2}{8^2}}=\frac{15}8$

$\displaystyle tgC=\sqrt{\frac{13^2-12^2}{12^2}} =\frac5{12}$

В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.

AK=8a/15; CN=12a/5

AC=AK+KN+NC=(44a/15)+b=44

P(KLMN)=2a+2b=59

Составим систему и определим S(KLMN)=ab

$\displaystyle \left \{ {{\frac{44}{15}a+b=44\;|\cdot 2} \atop {2a+2b=59\qquad }} \right.-\\\\\frac{88-30}{15} a=88-59\Leftrightarrow a=7,\! 5$

b=(59-15)/2=22

ab=7,5·22=165

Теперь всё тоже самое только AC=2√421.

В ΔABC по теореме косинусов:

$\displaystyle \cos A=\frac{17^2+4\cdot 421-39^2}{2\cdot 2\sqrt{421}\cdot 17} =\frac{113}{17\sqrt{421}}$

$\displaystyle \cos C=\frac{4\cdot 421+39^2-17^2}{2\cdot 2\sqrt{421}\cdot 39} =\frac{243}{13\sqrt{421}}$

По формуле связи косинуса и тангенса:

$\displaystyle tgA=\sqrt{\frac{17^2\cdot 421-113^2}{113^2}}=\frac{330}{113}$

$\displaystyle tgC=\sqrt{\frac{13^2\cdot 421-243^2}{243^2}}=\frac{110}{243}$

AK=113a/330; CN=243a/110

AC=AK+KN+NC=(421a/330)+b=2√421

P(KLMN)=2a+2b=59

$\displaystyle \left \{ {{\frac{421}{330}a+b=2\sqrt{421}\; |\cdot 2} \atop {2a+2b=59}\qquad \qquad } \right. -\\\\\frac{842-660}{330}a=4\sqrt{421}-59\\\\a=\frac{165}{91}(4\sqrt{421}}-59)$

Заметим, что проекция AB на AC равна AB·cosA=113/√421

Получается, что AK=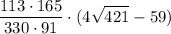$\displaystyle \frac{113\cdot 165}{330\cdot 91}\cdot (4\sqrt{421}-59)$ > 113/√421.

Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.

ответ: 165.