1) Радиус любой окружности в два раза меньше её диаметра.
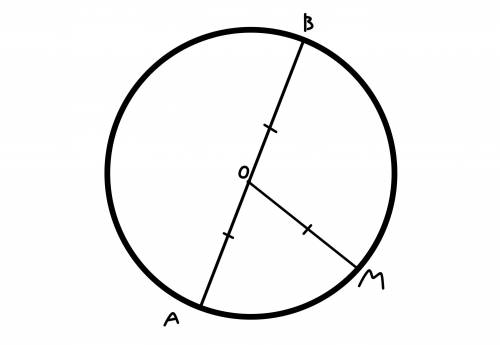
Пусть на рисунке О - центр окружности.
АВ - диаметр.
ОМ - радиус = 10,5 см.
Тогда, АВ = 2*ОМ = 2*10,5 см = 21 см.
Диаметр равен 21 см.
2) Нет, хорда данной окружности не может быть равна 22 см. Диаметр - это самая большая хорда окружности. Все диаметры равны. Мы уже нашли диаметр, он равен 21 см. Следовательно, мы никак не сможем провести хорду, равную 22 см.
Два решения
1)
Из треугольников ABC, ACD соответственно по теор синусов
CAB=a
CAD=b
BC/sina=AC/sin(a+2b)
CD/sinb=AC/sin(2b+a)
но BC=CD , тогда
sina/sin(a+2b) = sinb/sin(b+2a)
sina*sin(b+2a) - sinb*sin(a+2b) = 0
cos(a-b-2a)-cos(b+3a) - cos(b-a-2b)+cos(a+3b)=0
cos(a+3b)=cos(b+3a)
a+3b=b+3a
2b=2a
a=b
CAB=CAD
2)
Пусть AECF точка O пересечения диагоналей и OE=OF рассмотрим симметрию относительно точки O, точка Е перейдет в точку F, точка B в точку D по определению симметрии так как CB=CD точка А перейдет в себя, тогда AB=AD тогда треугольники ABC=ACD откуда
180-2a-b=180-2b-a
3a=3b
a=b
D = 2R = 10.5 * 2 = 21 см
Хорда всегда меньше или равна диаметру (кстати диаметр это максимальная хорда). D = 21 см, => хорды 22 см не может быть.