1 В окружности с радиусом 12 см проведена хорда длиной 12 см. Чему равны длины стягиваемых ею дуг? Найти площадь полученного сегмента [4]
2 Хорды MN и пересекаются в точке K. Найти DK, если MK = 3 см, NK = 8 см, K = 4 см.[4]
3 Найди площадь круга, вписанного в равнобедренную трапецию с основаниями длиной 4 см и 10 см и периметром 24 см.
-сторона основания,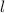 
- апофема, 
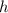- высота основания. Эти три величины потребуются для всего вычисления.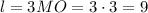
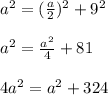
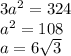
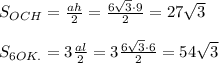
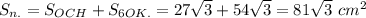
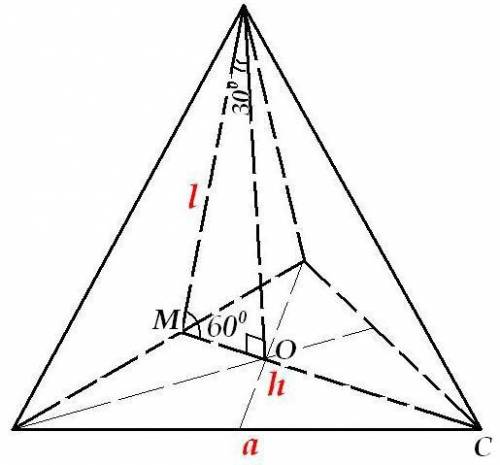
См. рис.
Так как AD - диаметр окружности, то угол ∠ABD = 90°
Следовательно, оставшийся угол прямоугольного
треугольника ΔABD: ∠BAD = 90 - 65 = 25°
Так как угол ∠BAD - вписанный, то величина дуги, на которую он опирается:
∪BCD = 2 · ∠BAD = 50°
Искомый угол ∠С = ∠BCD опирается на оставшуюся дугу
окружности:
∪BAD = 360 - ∪BCD = 360 - 50 = 310°
И величина угла ∠С = 310 : 2 = 155°
Причем, величина угла ∠С не зависит от местоположения точки С на дуге ∪BCD, так как в любом случае этот угол опирается на дугу ∪BAD, равную 310°