Задача
Дано:
периметр равностороннего треугольника 18 см
периметр равнобедренного треугольника 20 см
Сторона равностороннего треугольника является основанием равнобедренного треугольника
Найти: стороны равнобедренного треугольника
Решение
1) 18:3=6 (см) - сторона равностороннего треугольника;
2) пусть боковые стороны равнобедренного треугольника равны х см, тогда
х +х + 6 = 20
2х=20-6
2х=14
х=7 (см) - боковые стороны равнобедренного треугольника;
ответ: стороны равнобедренного треугольника равны 6 см, 7 см и 7 см.
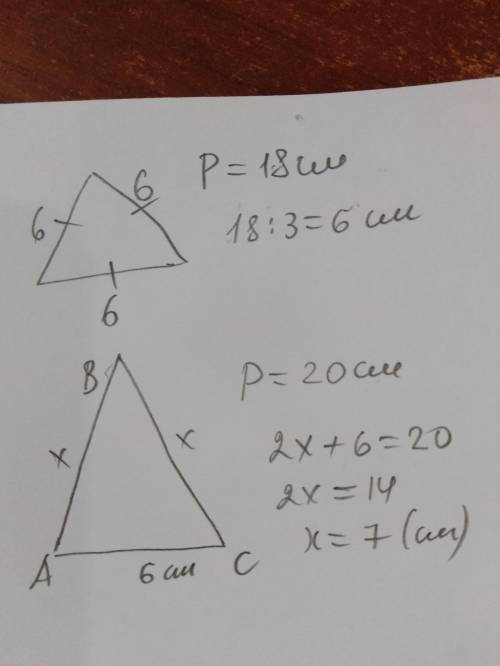
Высота этого треугольника МК=10 см по условию.
АК/МК = tg(30°)
АК = 10tg(30°) = 10/√3 см
АВ = 20/√3 см
Площадь основания - половина произведения диагоналей
S₁ = 1/2*(АВ)² = 1/2*400/3 = 200/3 см²
---
Сторона основания
S₁ = a²
a² = 200/3
a = √(200/3) = 10√(2/3) см
Половина основания
a = 5√(2/3) см
Половину основания и боковую сторону мы знаем, по Пифагору найдём апофему f
f² + (5√(2/3))² = (20/√3)²
f² + 25*2/3 = 400/3
f² = 350/3
f = 5√(14/3) см
Площадь боковой грани
S₂ = 1/2*a*f = 1/2*5√(2/3)*5√(14/3) = 25√7/3 cм²
И полная поверхность
S = S₁ + 4S₂ = 200/3 + 4*25√7/3 = 100/3(2 + √7) см²