Угол АОЕ равен 34 градуса.
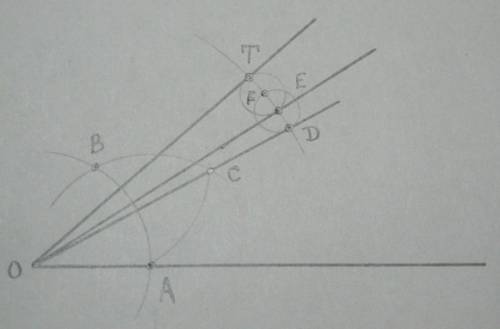
Откладываем на луче ОА произвольный отрезок ОА, на котором строим равносторонний треугольник АОВ. Тогда угол ВОА равен 60 градусов. Построим биссектрису угла ВОА - ОЕ, а значит угол АОЕ будет равен 30 градусов.
Угол ЕОД равен разности углов ЕОА и DOA 34-30=4 градуса.
4*3=12 градусов, для такого построения на луче ОD отложим произвольный отрезок OD. Проведем окружность радиусом OD и с центром в точке О.
Получим точку пересечения этой окружности с лучем ОЕ в точке Е.
Расположим одну ножку циркуля в точку Е, а другую в точку D.
Построим окружность радиусом ED и центром в точке Е.
Эта окружность даст точку пересечения F.
Построим ещё одну окружность с этим радиусом, но с центром в точке F.
Получим ещё одну точку пересечения Т.
Таким образом мы отложили три раза угол по 4 градуса.
Итого: получили угол ТОD в 12 градусов
ответ: построить такой угол можно
Обозначим ромб АВСД, большая диагональ АС=24 см. меньшая диагональ ВД.
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам. Диагональ АС делится на отрезки АО и ОС по 12 см.
Периметр ромба = 60 см, следовательно каждая сторона равна 60 : 4 = 15см (все стороны равны)
Так как диагонали перпендикулярны, то треуг АОВ прямоугольный. АВ=15 см гипотенуза, АО=12см (катет). По теореме Пифагора найдём катет ВО, который является частью меньшей диагонали ВД.
ВО ^2=225-144=81
ВО=9 см
Значит вся диагональ равна 18 см
ответ. 18 см
1)120°
2)65°
3)60°
4)"="
Объяснение:
1) х угол при основании, их два; 4х угол при вершине; всего х+х+4х=6х и это 180°=> х=30
угол при вершине 4*30=120
2) (180-50)/2=130/2=65
3) в равностороннем треугольнике углы по 60°
биссектрисы их делят пополам, т.е. 30°
При пересечении биссектрис образуется треугольник, в котором 2 угла по 30°, отсюда 180°-30°*2=120°, но этот угол тупой. Острый угол является смежным с ним. Сумма смежных углов равна 180°, значит острый угол равен 180°-120°=60°
4) т.к. периметр это сумма всех сторон, а медиана, разбивая треугольник АВС на 2 треугольника(АМВ и АМС) является общей стороной и предполагает, что ВМ=СМ, то при равных периметрах третьи стороны равны.