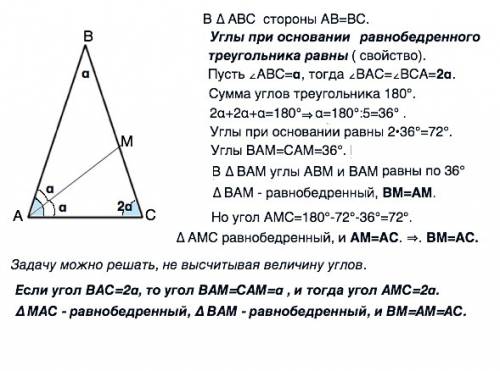
В ∆ АВС стороны АВ=ВС. Углы при основании равнобедренного треугольника равны ( свойство).
Пусть ∠АВС=α, тогда ∠ВАС=∠ВСА=2α.
Сумма углов треугольника 180°. 2α+2α+α=180° α=180°:5=36° .
Углы при основании равны 2•36°=72°.
Углы ВАМ=САМ=36°. В ∆ ВАМ углы АВМ и ВАМ равны по 36°.
∆ ВАМ - равнобедренный, ВМ=АМ.
Но угол АМС=180°-72°-36°=72°.
∆ АМС равнобедренный, и АМ=АС. ⇒. ВМ=АС.
-------
Задачу можно решать, не высчитывая величину углов.
Если угол ВАС=2α, то угол ВАМ=САМ=α , и тогда угол АМС=2α.
∆ МАС - равнобедренный, ∆ ВАМ - равнобедренный, и ВМ=АМ=АС.
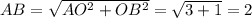
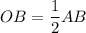⇒ ∠BAC = 30°, т.к. напротив угла в 30° лежит катет, равный половине гипотенузы.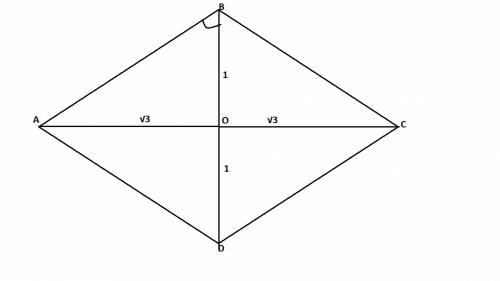
1) Площадь бок.пов-сти прав. пирамиды равна S = 0,5*P*h, где Р-периметр основания, h - апофема. Таким образом надо знать сторону основания и высоту боковой грани.
Рассмотрим тр-к SOD- прям.: L OSD=30 град.. Построим ср.линию MN того тр-ка, соединяющую середины сторон ОS и SD.
Тогда OD = 2*MN =2* корень из 3.
Значит h= SD =2*OD= 4* корень из 3 ( !апофема), т.к. в прям. тр-ке
напротив угла 30 град.,лежит катет , который в 2 раза меньше гипотенузы.
2) Найдём сторону основания: OD - радиус вписанной окружности, тогда
АВ= 2*OD*корень из 3= 2* 2*корень из 3* корень из 3 =12
Р =3*12=36, таким образом
S = 0,5*P*h= S = 0,5*36*4*корень из 3 = 72*корень из 3 (кв.ед).
ответ: 72*корень из 3 кв.ед.