сторона квадрата равна 10 как и высота призмы..хорошо
d = a√2 = 10√2(диагональ стороны квадрата)
R = d/2 = 10√2 / 2 = 5√2(радиус окружности)
S бок цилиндра = 2πR * H = 2*π*5√2*10 = 100π√2
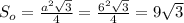- площадь основания
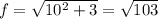см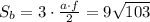
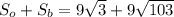
Объяснение:
1)Точки F и E-середины сторон BC и BA треугольника ABC.
Отрезок, соединяющий середины двух сторон треугольника, является его средней линией, равен половине третьей стороны и параллелен ей.
АЕ=ВЕ=10 => АВ=10•2=20 см
CF=BF=> ВС=16•2=32 см
АС=EF•2=14•2=28 см.
Периметр треугольника - сумма длин его сторон.
Р(АВС)=20+28+32=80 см
Вариант решения.
Так как отрезок ЕF – средняя линия ∆ АВС и параллелен АС, углы при основаниях ∆ АВС и ∆ ВЕF равны как соответственные углы при пересечении параллельных прямых секущими АВ и СВ, и угол В - общий.
Поэтому ∆ АВС~∆ ВЕF по равным углам.
АВ=2•ВЕ=>
Коэффициент подобия этих треугольников равен АВ:ВЕ. k=2
Р(BEF)=BE+BF+EF=40 см
Отношение периметров подобных фигур равно коэффициенту подобия их линейных размеров. ⇒
Р(АВС)=2Р(BEF)=2•40=80 см
2) Примем меньшее основание трапеции равным а. Тогда большее – 2а
Средняя линия трапеции равна половине суммы оснований.
6=( а+2а):2
а+2а=12
3а=12 ⇒ а=12:3=4
Меньшее основание трапеции равно 4 см.
Большее 4•2=8 см
правильная четырехугольная призма подразумевает в своем основании квадрат..
значит сторона квадрата равна 10 как и высота призмы..хорошо
зная сторону квадрата найдем его диагональ она равна : d = a√2 = 10√2
так как основание описана окружностью, то найдем радиус оп.окружности:
R = d/2 = 10√2 / 2 = 5√2
S бок цилиндра = 2πR * H = 2*π*5√2*10 = 100π√2