Для решения применим теорему Фалеса: Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Чтобы без линейки с делениями разделить отрезок, длина которого не известна, нужно от одного из концов этого отрезка провести под углом к нему вс луч и на этом луче на равном расстоянии отметить нужное количество точек.
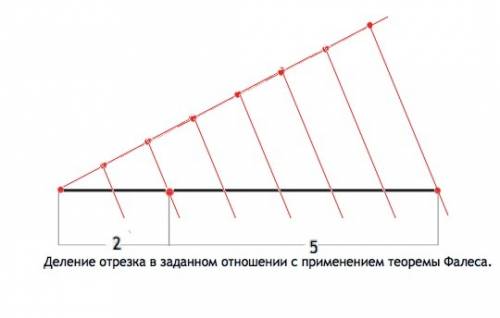
а) На вс луче отложим через равные промежутки 2+5 =7 точек. Затем через последнюю точку и конец заданного отрезка проведём прямую и через все точки ещё 6 прямых, параллельных ей. При этом заданный отрезок будет разделен на 7 равных частей. Отсчитаем 2 из получившихся отрезков. Остальная часть равна 5 отмеренным отрезкам, а исходный разделен в отношении 2:5
Можно на заданном отрезке откладывать не 7 отрезков, а провести всего 2 прямые - через седьмую и параллельно ей через вторую точку. Заданный отрезок будет разделён в нужном отношении.
б) и в) делим точно так же.
Объяснение:
Задача 1:
Так как сумма углов прилежащих к одной стороне равна 180 градусов, значит углы данные в задаче- противолежащие. Противолежащие углы у параллелограмма равны, следовательно:
A + C= 62 равно 2A=62
Пусть A=x, тогда
2x=62
x=31 градус = угол А и следовательно=уголу C (противолежащие углы парал. равны)
Сумма прилежащих к одной стороне углов равна 180 градусов, следовательно, угол B= 180-A=180-31=149 градусов
ответ: угол B=149 градусов
Задача 2:
Так как противолежащие углы параллелограмма равны, а сумма углов прилежащих к одной стороне равна 180, то можно составить уравнение
Пусть угол A - x. Тогда угол D=x+70
x+(x+70)=180
2x+70=180
2x=110
x= 55- градусов угол A
1) D=180 - A= 180-55=125 градусов
ответ: 125 градусов = угол D