Сторона меньшего основания правильной треугольной усечённой пирамиды равна 2 см, а боковое ребро пирамиды, равное √2 см , образует со стороной большего основания угол 45° . Найдите полную поверхность пирамиды.
Объяснение:
S( полное)=S(в.осн.)+S(н.основ)+S(бок) ,
1) S(прав.треуг.)=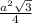
, S(в.осн.)=
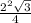=√3 (см²).
2)Боковые грани - равнобедренные трапеции . Пусть в трапеции
ВСС₁В₁ отрезки В₁Н, С₁К- высоты. Тогда ΔВВ₁Н-прямоугольный ,равнобедренный (∠ВВ₁Н=90°-45°=45°)⇒ВН=В₁Н=х. По т. Пифагора х²+х²=(√2)² ,х=1. Значит В₁Н=1 , ВС=ВН+НК+КС=1+2+1=4 (см).
3) S(н.осн.)=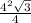
=4√3 (см²).
4)S(бок) =3*S(трапеции ВСС₁В₁) =3* 1/2*В₁Н*(ВС+В₁С₁)=3*1/2*1*6=9(см²).
5)S( полное)=√3 +4√3 +9=9+5√3 ( см²) .
Коэффициент подобия называется отношение любых соответственных линейных размеров первой фигуры к линейным размерам второй фигуры, находящимся против одинаковых углов.
А так как площадь треугольника равна произведение сторон АВ, ВС, и синуса угла между ними, а А1В1 = к * АВ, В1С1 = к * ВС, к коэффициент подобия,то :
S A1B1C1 = A1B1 * B1C1 * sin <(A1B1,B1C1) = 81 (cм2) = к* АВ * к * ВС * sin<(AB,BC) = k^2*S ABC
S ABC = AB * BC * sin < (AB,BC)=25(cм2).
к^2 = S A1B1C1/ S ABC = 81/25, k = 9/5 = 1,8
^ - степень
/ - деление