Точка равноудалённая от катетов образует внутри прямоугольного треугольника квадрат со стороной а, вершины которого - вершина прямого угла, точка на гипотенузе и две точки на катетах, от которых равноудалена заданная. Внутри прямоугольного образовались квадрат и два подобные между собой прямоугольных треугольника, которые подобны исходному треугольнику . пусть Один из катетов прямоугольного треугольника(1) - х и гипотенузой - 40 см, тогда соответствующий катет прямоугольного треугольника(2) - а см и гипотенузой - 30 см. Составим систему уравнений: Тогда один катет исходного прямоугольного треугольника - х+а=56 см. Второй катет по теореме Пифагора: = 1764, второй катет равен
1)
Если трапеция равнобедренная, то АБ=СД=5, следовательно АБ+СД=10.
Тогда сумма двух оснований равна 32-10=22.
Площадь равна средняя линия * h(высоту)
Ср линия = 22/2=11.
Из формулы площади найдем высоту:
h=S/ср.лин
следовательно высота равна 44/11=4
ответ: h=4
2)
S(трапецииABCD) = (AD + BC) : 2 * h
h - высота трапеции и треугольника ACD
S(ACD) = 1/2 * AD * h, следовательно
h = S(ACD) / (1/2 * AD) = 30 / (1/2 * 10) = 30 : 5 = 6 см
S(трапецииABCD) = 1/2*(10 + 8) * 6 = 9 * 6 = 54 см²
P.S. 1/2 -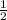
/ - дробь