Длины всех ребер правильной шестиугольной призмы равны. Вычислителе длину большей диагонали призмы, если известно, что площадь боковой поверхности призмы равна 96 см².
Площадь боковой поверхности правильной шестиугольной призмы находится по формуле:
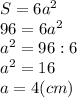
а - ребро нашей призмы.
Обратим внимание на чертеж. Искомая длина большей диагонали есть длина гипотенузы прямоугольного треугольника АА₁D.
AD = 2 * 4 = 8 (см)
По теореме Пифагора:
с² = a² + b²
AD₁² = AD² + DD₁²
AD₁² = 8² + 4²
AD₁² = 64 + 16
AD₁² = 80
AD₁ = √(16*5) = 4√5 (см)
ответ: 4√5 см

sin(a/2)=(d2/2)/m => (d2/2)=m*sin(a/2) => d2=2m*sin(a/2)
cos(a/2)=(d1/2)/m => (d1/2)=m*cos(a/2) => d1=2m*cos(a/2)
Sосн=d1*d2/2=2m*sin(a/2)*2m*cos(a/2)/2=2m^2*sin(a/2)*cos(a/2)=m^2*sin(a)
sin(b)=h/d1 => h=d1*sin(b) => h=2msin(a/2)*sin(b)
Sпп=p*h+2Sосн = 4m*2msin(a/2)*sin(b) +2*m^2*sin(a) = =8m^2*sin(a/2)*sin(b)+2*m^2*sin(a)