1200√3 см²
Объяснение:
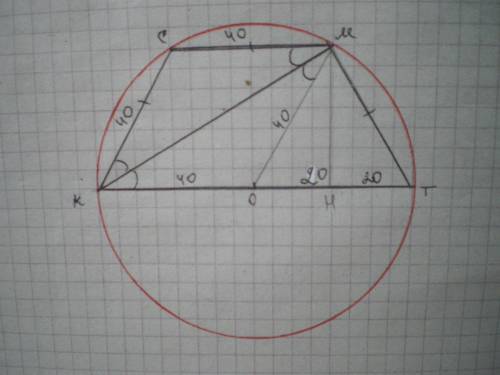
Дано: КСМТ - трапеція, КС=МТ, ∠КМТ=90°, КМ - бісектриса, ОМ=КО=ОТ=40 см. Знайти S(КСМТ).
∠КМТ - прямий, отже він спирається на діаметр описаного кола, тоді КТ=КО+ОТ=80 см.
∠СКМ=∠ТКМ за умовою, ∠СМК=∠ТКМ як внутрішні при СМ║КТ і січній КМ, отже ∠КСМ=∠СКМ, а ΔКСМ - рівнобедрений, КС=СМ.
Проведемо радіус ОМ=40 см, ΔКОМ=ΔКСМ за двома кутами і спільною стороною, отже КС=СМ=КО=ОМ=40 см.
МТ=КС=40 см.
ΔОМТ - рівнобедрений, проведемо МН - висоту і медіану.
ОН=ТН=40:2=20 см
За теоремою Піфагора МН=√(МТ²-ТН²)=√(1600-400)=√1200=20√3 см.
S(КСМТ)=(СМ+КТ):2*МН=(40+80):2*20√3=1200√3 см²
Требуется по известному объёму шара, равного 36 * π см3, определить площадь поверхности сферы, которая ограничивает этот шар.
Как известно, объём шара (V) при известном радиусе R, вычисляется по формуле V = (4/3) * π * R3.
Согласно условия задания, имеем, (4/3) * π * R3 = 36 * π см3, откуда R3 = (36 * π см3) : ((4/3) * π) = 27 см3.
Последнее равенство позволяет определить длину радиуса шара (что тоже самое, длину радиуса сферы, которая ограничивает шар): R = 3 см.
Теперь легко вычислить площадь (S) поверхности сферы по формуле: S = 4 * π * R2 .
Имеем: S = 4 * π * R2 = 4 * π * (3 см)2 = 4 * π * 9 см2 = 36 * π см2 .
ответ: 36 * π см2.