1)В прямоугольном треугольнике сумма острых углов равна 90 градусам
2) В прямоугольном треугольнике катет лежащий против угла в 30°, равен половине гипотенузы.
3)В прямоугольном треугольнике если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
4) Один из острых углов прямоугольного треугольника в 2 раза больше другого. Найдите острые углы этого треугольника
Пусть один угол -х, тогда другой - 2х, а т.к. Δ прямоугольный, то третий угол =90°. Сумма углов треугольника =180°
90+х+2х=180
3х=180-90
3х=90
х=30° один угол
30*2=60° второй угол
5) Один из углов прямоугольного треугольника на 18° больше другого . Найти величины всех углов треугольника
180-сумма
x-один угол
x+18-другой
90+18+х+х=180
2х+108=180
2х=72
х=36
Значит, 90°-один угол,36°-второй,54°-третий
6)Существует ли треугольник с двумя прямыми углами? - Нет, сумма углов треугольника всегда 180 градусов.
7) В прямоугольном треугольнике сумма острых углов равна 90°
8) Сторона прямоугольного треугольника, лежащая против большего угла называется гипотенузой.
9.Если катеты одного прямоугольного треугольника соответственно равны катетом другого, то такие прямоугольные треугольники равны.
10) В прямоугольном треугольнике один из острых углов равен 30°,а противолежащий ему катет равен 6см. Сторона, лежащая против угла 30° в 2 раза меньше гипотенузы, то есть она равна 12 см.
11) Углы равнобедренного прямоугольного треугольника равны 60°,60°,60°.
12) Сторона прямоугольного треугольника , лежащая против острого угла называется катет.
13) В треугольнике АВС угол С равен 90○,угол В равен 60○,СВ =6 см. Сторона АВ равна 12 см
т.к угол С= 90 градусов,угол В= 60 градусов,=> угол А=90-60=30 градусов,а тк против угла А=30 градусов лежит сторона СВ=6 см,а против угла в 30 градусов лежит стороны = 1/2 гипотенузы,тогда АВ= 6 *2=12 см сторона АВ
14) В треугольнике АВС угол С равен 90° , АВ= 15см ,СВ=7,5см . Угол В равен 60°
Катет СВ равен половине гипотенузы, значит он лежит против угла30°,
т.е угол А равен 30°Следовательно угол B равен 60°
15) Перечислите все признаки равенства прямоугольных треугольников (коротко):
1) по двум катетам;
2) по катету и гипотенузе
3) по гипотенузе и острому углу
4) по катету и острому углу
Задачи №1 - №3 решены Пользователем Fialka7 Умный
Добавлено решение задачи №4.
№1
Р = 36 см . Находим боковые стороны - они равны, значит а=(36-10)/2=13 см. Проводим высоту к основанию ВН. ВН²=13²-(10/2)²=144=12². S=BH*AC*1/2=12*10/2=60cм²
№2.
Р=24=а*4 а=6 см -сторона ромба. S=a²*sinA 18=36*sinA sinA=1/2 ∠А=30°, другой угол= 180-30=150°. ответ: 30°, 150°, 30°,150°.
№3
ищем сторону а. а=(128-48)/2=40см -боковая сторона. r=S/p где р-это полупериметр. р=128/2=64. Ищем S. Проведем высоту ВН.
ВН²=40²-24²=1024=32². BH=32 см, S=32*48*1/2=768 см². r=768/64=12 см. ответ: 12 см.
№4
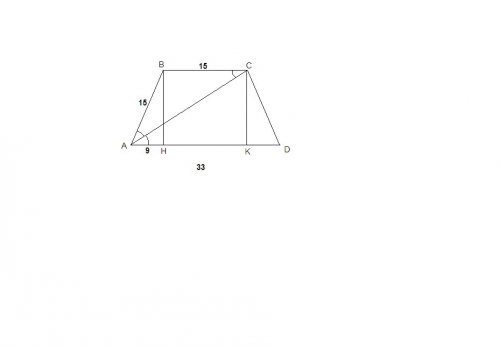
∠BAC = ∠DAC так как диагональ АС является биссектрисой угла А,
∠DAC = ∠BCA как накрест лежащие при пересечении параллельных прямых ВС и AD секущей АС, ⇒
∠ВАС = ∠ВСА, ⇒ ΔАВС равнобедренный, АВ = ВС = 15 см.
Отрезки, отсекаемые высотами равнобедренной трапеции на нижнем основании, равны полуразности оснований:
АН = (AD - BC) / 2 = (33 - 15)/2 = 9 см.
ΔАВН: ∠АНВ = 90°, по теореме Пифагора:
ВН = √(АВ² - АН²) = √(15² - 9²) = √144 = 12 см
Sabcd = (AD + BC)/2 · BH = (33 + 15)/2 · 12 = 288 см²
Т.к. противоположные стороны параллелограмма равны, т.е. AD=BC, а AM/AD=PC/BC=1/3, то МА=РС. также доказывается равенство AN=CQ. Т.о. треугольники MAN=PCQ по двум сторонам и углу между ними. следовательно MN=QP. Таким же образом доказывается равенство треугольников NBP=QDM и равенство отрезков QM=NP. Т.к. отрезки MN=PQ, а также NP=QM, следовательно, четырехугольник MNPQ является параллелограммом по попарному равенству противоположных сторон.