Объяснение:
попытка N2
геометрическая интерпретация задачи
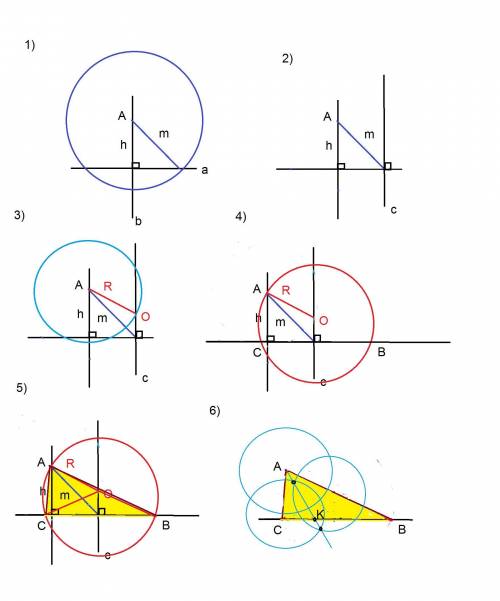
построить биссектрису треугольника по высоте h, медиане m, радиусу описанной окружности
(без описания элементарных построений)
1) строим 2 перпендикулярные прямые. на вертикальной откладываем высоту. Верхняя точка высоты - Вершина А треугольника.
из вершины как центра строим окружность радиуса = m
2) через точку пересечения медианы и горизонтальной прямой строим перпендикуляр к горизонтали (это прообраз серединного перпендикуляра к основанию треугольника)
3) из вершины А строим окружность радиуса R
точка пересечения этой окружности с перпендикуляром с будет центром описанной окружности О
4) строим окружность с центром О радиуса R
точки пересечения этой окружности с горизонтальной прямой - Вершины треугольника С и B
5) соединяем точки А, В, С
6) строим биссектрису АК угла А треугольника
готово.
P/S.
Теперь дело за формулами.
Возможно геометрическая интерпретация найти алгебраическую.
Если геометрическая интерпретация не совсем то что надо отметьте как нарушение.
В любом случае автору за интересную задачу
продолжение следует....
1) ∠AFD=90°, т.к. сумма углов при основании трапеции равна 90°;
2) ∠FEO=90°, т.к. Е - точка касания;
3) ОG⊥AB, т.к. OB и ОA равны как радиусы, а G - середина AB
Значит OEFG - прямоугольник, откуда радиус окружности OE=GF.
Т.к. треугольник AFD подобен BFC с коэффициентом подобия 36/12=3 и AB=10, то (BF+10)/BF=3, т.е. BF=5. Далее GB=10/2=5. И, значит,
OE=GF=GB+BF=5+5=10. Итак, радиус окружности равен 10.