решить

1. На отрезке АС находятся точки М и О, причем О-середина отрезка АС. Найдите длину МО, если АО=6

см, и МС меньше АМ на 3 см.

2. АД- биссектриса угла МАС, АВ - биссектриса угла МАТ, причем ВАТ равен 37%. Найдите величины

углов МАВ, ТАС, МАС.

3. Какой отрезок называется биссектрисой треугольника?

4. Найдите углы равнобедренного треугольника, если угол между биссектрисой и боковой стороной

составляет 32° (биссектриса проведена из вершины треугольника при основании).

5. Постройте треугольник по двум углам 40° и 35°, прилежащим к стороне вс=6 см. Опишите построение

и определите вид треугольника.

👇

Открыть все ответы

Ответ:

W1LDOR

27.09.2022

Хорошо, сведем задачу к нахождению диагонали трапеции т.к. есть формула S= d^2/2 * sinA где d- диагональ, синус угла 60 у нас есть он равен 1/2* корень из 3.
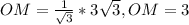
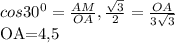
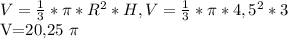
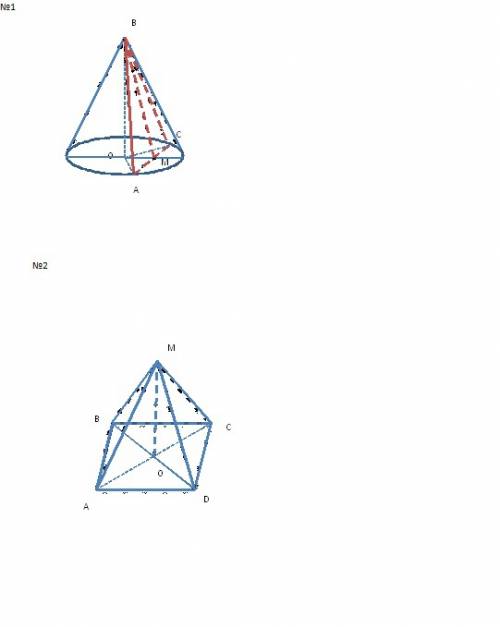
Диагонали в равнобедр. трапеции образуют собой равнобедр. треугольники AOD и BOC рассмотри треугольник ВОС:
угол ВОС равен 180- 60= 120, тогда углы при основании равны по 30 (углы ОСВ и ОВС)
далее возьмем прямоугольный треугольник АНС где АН- высота:
угол АСН мы нашли он равен совпадающему углу ОСВ и равен 30
тогда угол НАС равен
180-90-30=60
АН=2
найдем сторону НС:
по формуле НС = АН*tgА= 2* tg HAC= 2 * tg 60 = 2* корень из 3=
2 корня из 3
окей, далее найдем АС она же является диагональю трапеции:
АС= НС/sin НАС= 2 корня из 3/ ( 1/2* корень из 3) = 4
готово, осталось посчитать:
S = АС^2 /2 * sin 60= 8* корень из 3 /2 = 4 корня из 3 см в квадрате

4,6(15 оценок)

Ответ:

simpleam

27.09.2022

Сечение конуса - ΔАВС с основанием АС=6√3 - хорда.
равнобедренный ΔАОС (О - центр основания конуса): АО=ОС=R, <AOC=120°, <OAC=<OCA=30°, OM_|_AC, ОМ - высота, медиана ΔАОС, ⇒АМ=3√3.
tg30°=OM:AM.

$OM= \frac{1}{ \sqrt{3} } *3 \sqrt{3} , OM=3$

$cos30^{0} = \frac{AM}{OA}, \frac{ \sqrt{3} }{2} = \frac{OA}{3 \sqrt{3} } 

OA=4,5

$

по условию, секущая плоскость составляет с плоскостью основания угол 45°, ⇒ линейный угол ВАСМ - угол ВМО=45°. высота конуса Н=ОМ=3

$V= \frac{1}{3}* \pi * R^{2}*H, V= \frac{1}{3} * \pi * 4,5^{2} *3

V=20,25 \pi 
 
$
ответ: Vк=20,25π

2. MABCD - правильная пирамида с диагональю основания АС=d, угол между боковым ребром МА и плоскостью основания <MAC= α
MO_|_(MABCD), МО - высота пирамиды.
прямоугольный ΔМОА: ОА=d/2, <A=α. tgα=MO:OA, MO=tgα*OA
MO=d*tgα/2

Vпир=(1/3)*Sосн*H
Sосн=a², a- сторона основания пирамиды
диагональ пирамиды найдена по теореме Пифагора из ΔАВС: АС²=АВ²+АС²
АВ=АС=а
d²=a²+a², d²=2a². d=a√2, ⇒a=d/√2
S=(d/√2)²=d²/2
Vпир=(1/3)*(d²/2)*(d*tgα/2)
Vпир=(d³ *tgα)/12

Решить (с рисунком) 1)через вершину конуса проведена плоскость пересекающая окружность основания по