Поскольку фокусы гиперболы лежат на оси абсцисс симметрично относительно начала координат, то это стандартная гипербола, которая имеет уравнение:
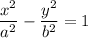, где а - действительная полуось, b - мнимая полуось
Поскольку дана точка гиперболы, то подставим ее координаты в уравнение:
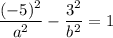
Также распишем эксцентриситет гиперболы:
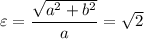
Преобразуем. Возведем в квадрат:
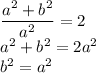
Подставим в уравнение с координатами выявленное соотношение:
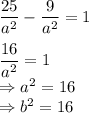
Все необходимые данные для записи уравнения есть:
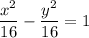
Поскольку квадрат мнимой полуоси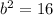 
, то ее длина - соответственно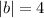 
а) параллельную данной прямой.
Из центра окружности опустить перпендикуляр на данную прямую.
Он пересечёт окружность в точке касания.
Через полученную точку провести прямую, перпендикулярную построенному перпендикуляру к данной прямой.
Эта прямая будет параллельна данной прямой.
б) перпендикулярную к данной прямой.
Из центра окружности опустить перпендикуляр на данную прямую.
Из центра окружности восстановить перпендикуляр к построенному перпендикуляру.
Он пересечёт окружность в точке касания.
Через полученную точку провести прямую, перпендикулярную к данной прямой.
Эта прямая и будет перпендикулярна данной прямой.
в) под данным острым углом к прямой.
В любой точке данной прямой построить прямую под заданным к ней углом.
Затем по пункту а) построить параллельную касательную прямую.