Обозначим наклонные L1=18 ; L2 = 2√109.
Проекции l1 = 3x ; l2= 4x
Пусть проекция точки А на плоскость – точка А1
АА1 – перпендикуляр к плоскости.
Между проекций и перпендикуляром прямой угол.
Наклонная, проекция и перпендикуляр образуют прямоугольный треугольник.
Наклонная – ГИПОТЕНУЗА
Проекция и перпендикуляр - КАТЕТЫ
Имеем два прямоугольных треугольника, с общей стороной – АА1.
По теореме Пифагора
АА1^2= L1^2-l1^2=18^2-(3x)^2 - для первого треугольника
АА1^2= L2^2-l2^2=(2√109)^2-(4x)^2 - для первого треугольника
Приравняем правые части
18^2-(3x)^2 = (2√109)^2-(4x)^2
324-9x^2 = 436-16x^2
7x^2= 112
X^2=16
X= 4
Тогда проекция l1=3x=3*4=12
АА1^2= 18^2-12^2 =180
AA1 =6 √5
ответ 6 √5
а) Координаты середины отрезка равны полусуммам соответствующих координат его концов.
А (2; -1; 0), В (-4; 2; 2)
Обозначим середину отрезка АВ буковой К
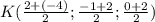
К (-1; 0,5; 1)
б) Нужно найти координаты точки С, если точка В является серединой отрезка АС. Координаты точек А и В известны. Координаты точки С обозначим (x; y; z). И используем формулу для нахождения координат середины отрезка. Находим координаты середины отрезка АС.
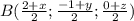
Координаты точки В известны. Приравняем их и получим три уравнения, решая которые найдем координаты точки С.
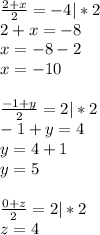
C (-10; 5; 4)
в) Длина отрезка можно вычислить так: квадратный корень из суммы квадратов разностей соответствующих координат концов отрезка.
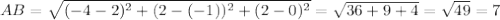
АВ=7
Пусть наклонные L1=18 ; L2 = 2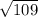 .
.
Проекции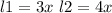
Пусть проекция А А1
АА1 – перпендикулярно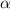
по т Пиф
тогда