АВ= 6 см, ВС= 8 см, угол между ними β= 60°.
Сначала найдём третью сторону треугольника.
По теореме косинусов:
AC²= AB² + BC² - 2•AB•BC•сosβ;
AC²= 36+64 - 2•6•8•½;
AC²= 100 - 48;
AC²= 52;
AC= 2√13 см ~ 7 см.
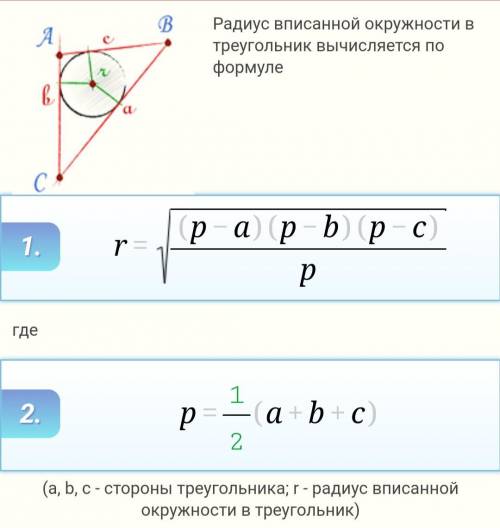
Формула радиуса вписанной в треугольник окружности во вложении.
Для того, чтобы его найти, сначала посчитаем полупериметр треугольника.
р= (АВ+ВС+АС)/2= (6+8+7)/2= 21/2= 10,5.
Находим радиус.
r²= (10,5 - 6)(10,5 - 8)(10,5 - 7) / 10,5;
r²= 4,5•2,5•3,5 / 10,5;
r²= 39,375 / 10,5;
r²= 3,75;
r= √3,75 ~ 1,9 (см)
P.S. Ужасные числа, но это верное решение...
Чтобы не писать лишние нули, меряю все в ДЕЦИМЕТРАХ :). Стороны AB = BC = 5, основание AC = 6. В конце ноль допишу :).
Пусть D - середина АС, BD - высота к основанию.
Высота к основанию делит треугольник на 2 "египетских" - прямоугольных со сторонами 3,4,5 (то есть высота к основанию BD = 4)
Центр окружности лежит на этой высоте, поэтому если её продлить до пересечения с описанной окружностью - пусть это точка Е - то BE - диаметр, BE = 2*R;
Треугольник ВАЕ подобен треугольнику BAD, поэтому
BD/AB = AB/BE;
4/5 = 5/(2*R);
R = 25/8;
Ну, или с САНТИМЕТРАХ
R = 250/8 = 125/4 ...
Интересно, что диаметр 125/2 = 60+2,5, то есть всего на 2,5 см длинее основания.