На стороне AB равностороннего треугольника ABC взята точка D так, что сумма расстояний от нее до сторон AC и BC равна 16 см. Найдите высоту треугольника, проведенную из вершины C.
РЕШЕНИЕ: Пусть сторона треугольника а. Одно из данных расстояний m, другое – n. Расстояния – это высоты. Находим площади треугольников:
Сюда относится картинка с умножением
Теперь их суммируем:
Сюда с сложением
В левой части полная площадь ABC, правую можно периписать так:
Сюда с сложением и умножением
Где h - высота из вершины C, равна сумме расстояний = 16 см
ОТВЕТ: 16 см
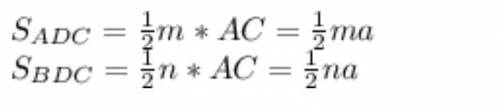
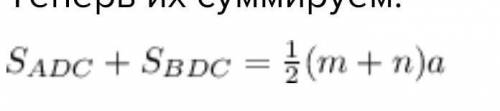
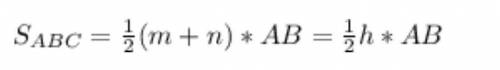
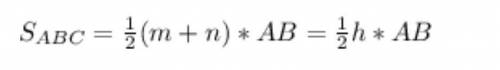
Сделаем рисунок, обозначим вершины углов трапеции привычными АВСД Через центр окружности проведем перпендикулярно к основаниям трапеции диаметр.
Его отрезок МК, заключенный между основаниями трапеции, является ее высотой и делит основания пополам. ( Основания - хорды, перпендикуляр из центра окружности к хорде делит ее пополам).
Соединим центр О с вершинами С и Д.
ОС=ОД=R
Обозначим ОК=х, тогда ОМ =27-х
По т. Пифагора
R²=МС²+ОМ²
R²=КД²+ОК² Приравняем значения радиуса.
МС²+ОМ²=КД²+ОК²
225+(27-х)²=576+х²
54х=378
х=7
ОК=7
R²=КД²+ОК²
R²=24²+7²
R²=625
R=25