DE = 24 см
Объяснение:
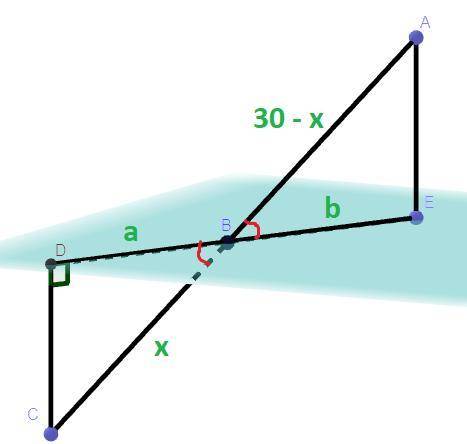
Дано: АС = 30 см, DC = 6 см, AE = 12 см, DC ⊥ ED, AE ⊥ DE
Найти: DE - ?
Решение: Пусть BD = a, BE = b. СB + AB = AC ⇒ AB = AC - BC = 30 - BC.
Пусть BC = x, тогда AB = 30 - x. Треугольник ΔCBD подобен ΔBAE по двум углам так как по условию DC ⊥ ED, AE ⊥ DE, то ∠CDB = ∠AEB = 90°, а углы ∠DBC = ∠ABE как вертикальные углы, из подобия треугольника ΔCBD треугольнику ΔBAE следует, что
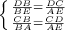
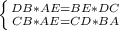
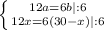
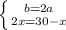
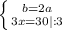
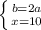
Рассмотрим треугольник ΔCDB. BD = x = 10 см. По теореме Пифагора:
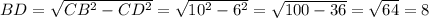 см.
см.
b = 2a ⇔ BE = 2BD = 2 * 8 = 16 см.
DE = BE + BD = 16 + 8 = 24 см.
∠ABC + ∠ACB = 180° - α
∠IBC + ∠ICB = (180° - α)/2 = 90° - α/2 (т.к. центр вписанной окружности лежит в точке пересечения биссектрис)
∠BIC = 180° - (∠IBC + ∠ICB) = 180° - 90° + α/2 = 90° + α/2
∠BKC = 180° - ∠BIC = 180° - 90° - α/2 = 90° - α/2 (сумма противоположных углов четырехугольника вписанного в окружность равна 180°)
∠BOC - центральный углу ∠BKC => ∠BOC = 2*∠BKC = 2*(90° - α/2) = 180° - α
т.к. ∠BAC + ∠BOC = α + 180° - α = 180°, то около ABOC можно описать окружность, но это та же окружность, которая описана около треугольника АВС и на ней лежит точка О. Что и требовалось доказать
ответ: доказано.