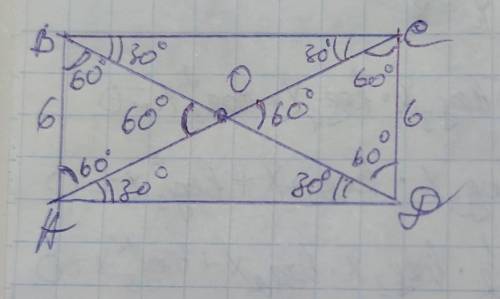
ответ: 12см
Объяснение: диагонали прямоугльника при пересечении делятся пополам образуя 2 равных равнобедренных треугольника АВО и СОД. Поскольку эти треугольники равнобедренные, то <АВО=<ВАО=<СДО=<ДСО. Сумма углов треугольника составляет 180°, поэтому сумма углов АВО и ВАО =180–60=120°, поскольку каждый из них равен, то <АВО=<ВАО=<СДО=ДСО=60°. Следовательно ∆АВО и ∆СДО - равносторонние. Рассмотрим полученный ∆АВС. Он прямоугольный где АВ и ВС - катеты, а АС - гипотенуза. Поскольку <ВАО и <ВАС является общим в ∆АВО и в ∆АВС, то <АСВ=90–60=30°, так как сумма острых углов прямоугольного треугольника составляет 90°. Катет АВ лежит напротив угла АСВ=30°, поэтому он равен половине гипотенузы АС, следовательно АС=6×2=12см. Диагонали прямоугльника равны, поэтому АС=ВС=12см
Введемо змінну Х та складемо рівняння:
2х + 3х + 4х = 180 (за теоремою про суму кутів трикутника)
9х = 180
х = 20
Тоді
2х = 40
3х = 60
4х = 80
Маємо кути трикутника 40, 60 і 80 градусів.
Зовнішні кути при вершинах трикутника дорівнюють 180 відняти прилеглий кут
Отже,
1-ий зовнішній кут = 180 - 40 = 140
2-ий зовнішній кут = 180 - 60 = 120
3-ій зовнішній кут = 180 - 80 = 100
Перевірка: сума зовнішніх кутів трикутника має дорівнювати 360 градусів:
140 + 120 + 100 = 360
Відповідь: зовнішні кути дорівнюють 140, 120, 100 градусів.