2) Диагонали BD i AC ромба равны 16 см и 12 см. Найдите сторону ромба.
Диагонали ромба точкой пересечения делятся пополам и пересекаются под прямым углом.
Следовательно, ромб пересечением диагоналей делится на 4 прямоугольных треугольника с катетами 8см и 6 см
Сторона ромба, как гипотенуза такого треугольника, найденная по теореме Пифагора,
равна 10 см.
Вообще, если катеты прямоугольного треугольника 8 и 6, можно сразу сказать, что гипотенуза - 10. Это египетский треугольник, соотношение сторон 3:4:5.
3) Боковая сторона равнобедренного треугольника = 13 см, а высота, проведенная к ней - 5 см. Найдите сторону треугольника.
( Примечание: Отношение сторон этого треугольника - тоже из числа так называемых "троек Пифагора". 5:12:13. Значит, второй катет прямоугольного треугольника, который образован боковой стороной, высотой и частью второй боковой стороны, равен 12.)
Но решаем классическим
Пусть дан равнобедренный треугольник АВС, в котором
АВ=ВС=13 см
Высота АД=5 см
Из прямоугольного треугольника АВД найдем отрезок ВД по теореме Пифагора.
ВД²=АВ²-АД²
ВД=√(169-25)=12
Тогда ДС=13-12=1
Из ⊿ АДС найдем гипотенузу АС
АС=√(АД²+ДС²)=√(25+1)=√26
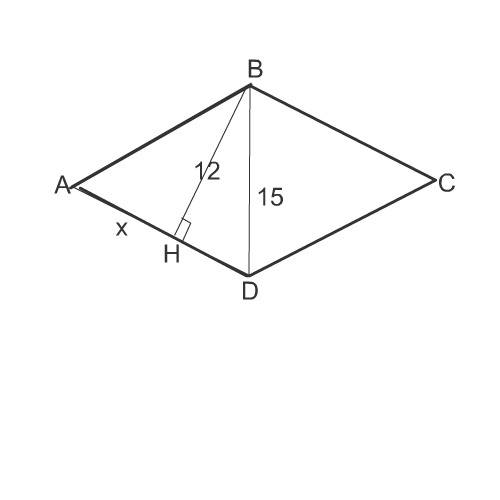
4) Высота ромба равна 12 см, а одна из его диагоналей - 15 см. Найдите площадь ромба.
Смотрим рисунок.
Стороны ромба равны.
АВ=АD
НD=√(ВD²-ВН²)=√(225-144)=9
Пусть АН=х
тогда
АВ=х+9
Из ⊿ АВН по теореме Пифагора
АВ²=АН² +ВН²
(х+9)²=12²+-х²
х²+18х+81= 144+ х²
18х=63
х =3,5
АВ=9+3,5= 12,5 см
Площадь параллелограмма ( ромб - параллелограмм) равна произведению выстоы на сторону, к которой она проведена.
S ABCD=12,5*12=150 см²
------------------------------------
1) Сумма острых углов трапеции равна 90град. Основы трапеции = 9 см и 16 см. Найдите высоту трапеции и длину боковых сторон.
Понятно, что эта трапеция - часть прямоугольного треугольника. Но острые углы в нем могут принимать любые значения и давать сумму 90 градусов, и основания будут при этом находиться друг от друга на разном расстоянии.
Единственное, что можно определить в этой ситуации - это сумма квадратов боковых сторон. Она всегда будет постоянной. Но не более.
.
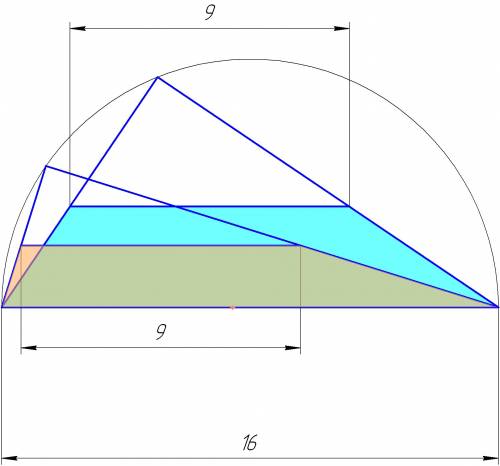
соединим концы хорд
получим четырехугольник
так как хорды параллельные - это вписанная равнобедренная трапеция
обозначим
R - радиус описанной окружности
c - боковая сторона трапеции
h = 42 высота трапеции
a = 36 и b = 48 - Основания
диагонали трапеции равны по теореме Пифагора
d^2 = h^2 + (a+(b-a)/2)^2 = 42^2 +(36 +(48-36)/2)^2 =3528
d = 42√2
боковая сторона
с^2 = h^2 + ((b-a)/2)^2 =42^2 +((48-36)/2)^2=1800
c = 30√2
диагональ(d), нижнее основание(b) и боковая сторона(c) образуют
треугольник , вершины которого лежат на той же описанной окружности
периметр треугольника P = b+c+d = 48+30√2+42√2=48+72√2
полупериметр треугольника p = 24+36√2
тогда радиус описанной окружности по известной формуле
R = (bcd) / 4√(p(p-b)(p-c)(p-d))=
=(48*30√2*42√2) / 4√((24+36√2)(24+36√2-48)(24+36√2-30√2)(24+36√2-42√2))= 30
ответ R=30
V=32√2
Объяснение:
Подробности в приложении.