Объяснение:
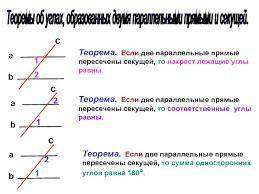
Теоремы с чертежами даны в первом рисунке
1)
a)56+32=/=180°; не параллельны
б)72=72; параллельны по накрест лежащим углам
в)113+67=180°; параллельны по сумме односторонних углов
г)153+35=/=180°; не параллельны
а)73+73=/=180°; не параллельны
б)25=/=63; не параллельны
в)58+22=/=180°; не параллельны
г)143=143; параллельны по накрест лежащим углам
2)
а) a║b
∠6=∠3=108°; ∠5=180-108=72°; ∠5=∠4=72°;
∠1=∠3=108°; ∠4=∠2=72°; ∠6=∠8=108°; ∠5=∠7=72°
б)m║d
∠4=∠6=63°; ∠3=180-63=117°; ∠3=∠5=117°; ∠7=∠5=117°; ∠6=∠8=63°; ∠2=∠3=117°; ∠1=∠4=63°
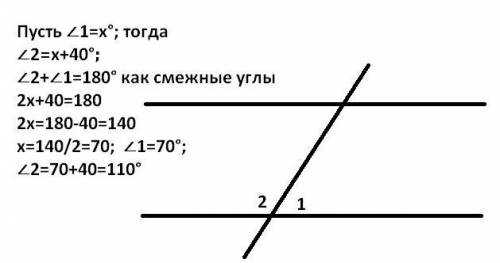
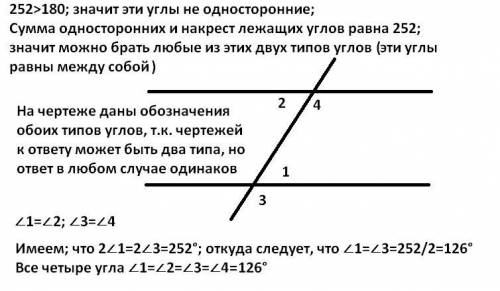
3) Решения даны на втором и третьем из прикреплённых рисунков
AC²=AB²+BC²-2*AB*BC*cos∠B
Известно, что АВ=ВС+4. Подставляем все известные значения в формулу:
14²=(ВС+4)²+ВС²-2(ВС+4)*ВС*cos120°
196=BC²+8BC+16+BC²-2(BC+4)*BC*(-1/2)
196=2BC²+8BC+16+BC²+4BC
3BC²+12BC-196+16=0
3BC²+12BC-180=0 |:3
BC²+4BC-60=0
D=4²-4*(-60)=16+240=256=16²
BC=(-4-16)/2=-10 - не подходит
BC=(-4+16)/2=6 см
АВ=6+4=10 см
ответ: АВ=10 см, ВС=6 см.