І нұсқа
1. Радиусы 5 см шеңбер центрінен түзуге дейінге қашықтық : а) 3 см; б) 5 см; в)
11 см болса, түзу мен шеңбердің өзара орналасу қалай болады?
2. Екі шеңбер сырттай жанасады. Бір шеңбердің радиусы екіншісінен 3 см қысқа.
Егер олардың центрлерінің ара қашықтығы 11 см болса, шеңберлердің диаметрлерін
табыңыз?
центрі оболатын шеңберді А және В нүктелерінде жанайтын түзулер с
нүктесінде өзара қиылысады. Егер ОАВО ОП40° болса, түзулер арасындағы
бұрышты табыңыз.
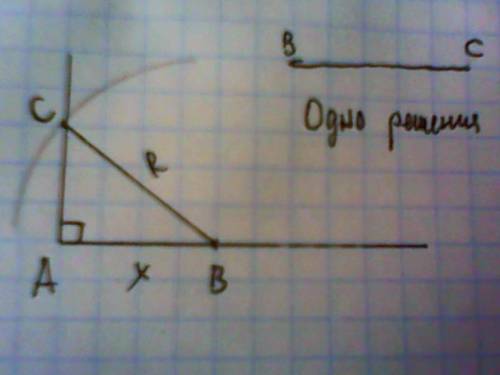
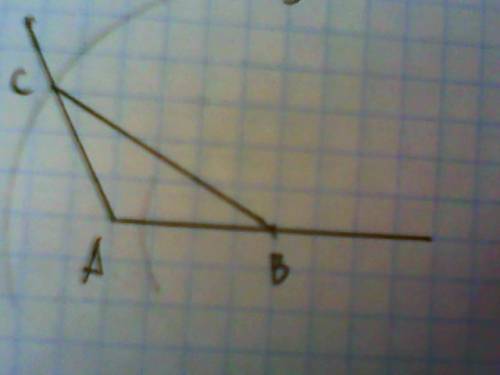
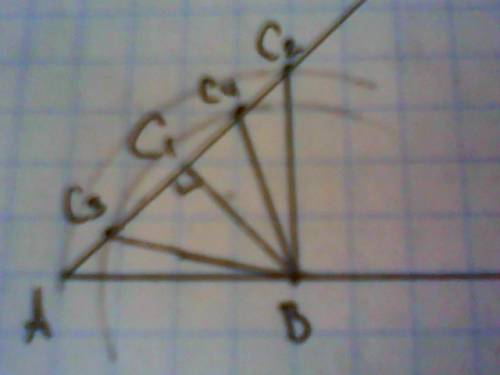
4. Екі тәсілмен ABC дұрыс үшбұрышын салыңыз.
Площади малых треугольников, отсечённых средними линиями в треугольниках с диагоналями в основании, равны одной четвёртой площадей этих треугольников (при коэффициенте их подобия k=2, коэффициент подобия их площадей k²=4).
Посчитаем площади отсечённых треугольников.
Обозначим площади треугольников с основаниями, лежащими на диагонали d₁ как S1 и S2, а треугольников с основаниями на диагонали d₂ как S3 и S4. площадь большого четырёхугольника обозначим S.
S=S1+S2 и S=S3+S4.
Площади отсечённых треугольников в первой паре: Sотс1=(S1+S2)/4=S/4.
Площади отсечённых треугольников во второй паре: Sост2=(S3+S4)/4=S/4.
Площади всех отсечённых треугольников: Sост=Sотс1+Sотс2=S/4+S/4=S/2.
Итак, площадь малого четырёхугольника: s=S-Sотс=S-S/2=S/2 - это ответ.
Можно немного проще.
Площадь произвольного четырёхугольника: S=(1/2)d₁·d₂·sinα, где α - угол между диагоналями.
Стороны малого четырёхугольника равны половинам диагоналей (мы это уже доказали).
Угол между соответственно параллельными прямыми равны, значит указанный угол между сторонами малого четырёхугольника равен α.
Площадь малого четырёхугольника (параллелограмма): s=ab·sinα=(d₁/2)·(d₂/2)·sinα=(1/4)d₁·d₂·sinα=S/2.
Всё!