Question

Abcdef - правильный шестиугольник, его площадь равна 60 см^2. найдите площади треугольников abc и acd. надо) заранее .

Answer 1

S = pr( р - это полупериметр многоугольника,r  это радиус вписанной окружности)

Пусть сторона шестиугольника равна а, тогда р = 3а, r =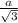$\frac{a}{\sqrt{3}}$

60 =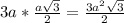 $3a*\frac{a\sqrt{3}}{2}}=\frac{3a^2\sqrt{3}}{2}$

$a^2 =\frac{40}{\sqrt{3}}$

S(АВС)= a*a*sin 120 =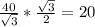 $\frac{40}{\sqrt{3}}*\frac{\sqrt{3}}{2}=20$

S(ACD)=30-20=10( Т. К  S ABC + S ACD  РАВНА ПОЛОВИНЕ ШЕСТИУГОЛЬНИКА)