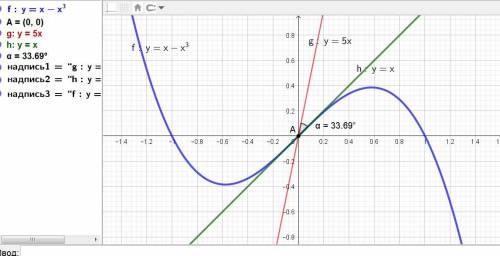
Даны кривая у = х - х^3 и прямая у = 5х
.
Находим их общую точку - точку пересечения.
Приравняем х - х^3 = 5х,
4x + х^3 = 0,
x(4 + x^2) = 0,
x = 0 один корень,
x^2 = -4 не имеет решения.
Угол между кривой и прямой равен углу между касательной к кривой и прямой.
Тангенс угла наклона касательной к оси Ох равен производной функции.
y' = 1 - 3x^2.
В точке х = 0 производная равна 1, то есть tg(fi) = 1.
Угол между прямыми находим по формуле:
tgα = (k2 - k1)/(1 + k2*k1) = (5 - 1)/(1 + 5*1) = 4/6 = 2/3.
α = arctg(2/3) = 0,5880 радиан или 33,690 градуса.
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник (свойство) => ВС=ВF=5.
AD=BC=5 (противоположные стороны параллелограмма). KD= КА+AD=4+5 = 9.
Треугольники KAF и KDC подобны (так как AF параллельна DC). Из подобия: KD/KA=CD/AF.
CD=AB, AF=x, CD=5+x. Тогда 9/4=(5+x)/x. =>
х = 4. АВ=CD=4+5=9.
Или так:
КА параллельна ВС => <CKA=<BCK как накрест лежащие. <KFA=<BFC (вертикальные)=<BCF =>
Треугольник KAF равнобедренный и AF=КА=4.
АВ=CD=5+4=9.
ответ: АВ=CD = 9. BC=AD=5.