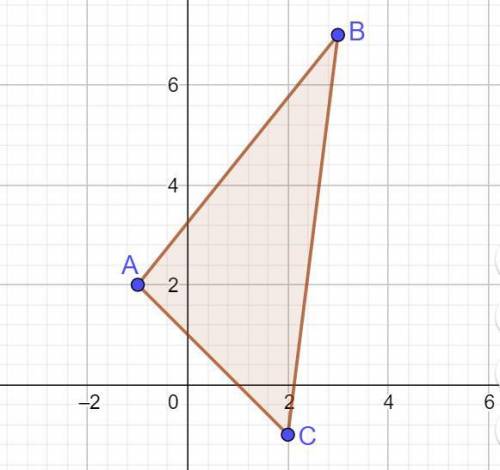
Даны вершины треугольника.
Точка А Точка В Точка С
х у х у х у
-1 2 3 7 2 -1
Находим длины сторон.
АВ ВС АС
Δx Δy Δx Δy Δx Δy
4 5 -1 -8 3 -3
16 25 1 64 9 9 квадраты
41 65 18 сумма квадратов
АВ (c) = 6,403 ВС(a) = 8,062 АС (b) = 4,243 .
Углы по теореме косинусов:
cos A = -0,110 A = 1,681 радиан 96,34 градусов
cos B = 0,852 B = 0,550 радиан 31,535 градусов
cos C = 0,614 C = 0,910 радиан 52,125 градусов .
ответ: треугольник тупоугольный.
1)
Треугольник AOB - Равнобедреный (т.к.АО=ОB) =>
угол OBA=30 °
OA- Радиус
OA ⊥ac
угол BAC=90°-30°=60°
ОТВЕТ:60°
надеюсь правильно
2)
◡АС=60°;◡АВ=◡СВ=150°
* * *
Сделаем и рассмотрим рисунок. Отметим центр окружности О. ОА=ОС=R.
Основание треугольника АС равно радиусу окружности. АС=R ⇒
∆ АОС - равносторонний, все его углы равны 60°.
Дуга окружности, на которую опирается центральный угол, равна его градусной мере. ◡ АС = ∠ АОС=60°. Полная окружность содержит 360°. ⇒ ◡АВ+ ◡СВ=360°-60°=300°. Т.к. ∆ АВС равнобедренный. хорды АВ=СВ. Равные хорды стягивают равные дуги. ◡АВ=◡СВ=300°:2=150°
3)
LM=R, OL=OM=R =>
∆ LOM- равносторонний.
Диаметр, проведенный перпендикулярно хорде, делит ее пополам. AL=AM=12,4 =>LM=2•12,4=24,8 см
D (EK)=2R=49,6 см
P(LOM)=3•LM=74,4 см
4) ΔABC - прямоугольный; ∠C = 90°; ∠B = 30°; AB = 10
Катет AC лежит против угла 30° ⇒ равен половине гипотенузы AB:
AC = AB/2 = 10 /2 = 5
Проведена окружность с центром в точке А
а) радиус в точку касания образует с касательной угол 90°.
a) Радиус равен АС = 5
б) радиус меньше 5
в) радиус больше 5
5 картинка