1. Точки A 1 i B 1 — проекцiї точок A i B на площину π. Пряма AB перетинає цю
площину в точцi C. Знайдiть довжину вiдрiзка AB, якщо AA 1 = 18см, BB 1 = 12см,
AC = 27 см.
2. Дано паралельні площини α і β. Через точку S, яка не належить жодній із них,
проведено прямі а і b, які перетинають площину α в точках A 1 і B 1 , а площину β —
в точках А 2 і B 2 , причому SA 1 = 8 CM, А 1 А 2 = 12 CM, A 2 B 2 = 25 CM. Знайдіть А 1 B 1 .
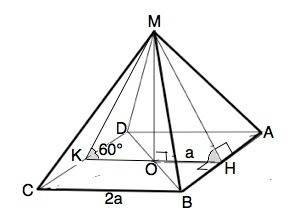
Обозначим пирамиду МABCD, М- вершина пирамиды. О - центр основания, МН - апофема.
----------
Примем сторону основания равной 2а.
Проведем КН через центр основания параллельно ВС.
ОН⊥АВ ⇒ МН⊥АВ ( по т. о 3-х перпендикулярах), ⇒
∠MHO=60°
∆ МОН - прямоугольный.
МН высота Δ МАВ
КН=ВС=2а,
ОН=КН:2=а
Высота МО=ОН•tg60°=a√3
Апофема МН=ОН:cos60°=2a
Площадь полной поверхности пирамиды
S=S₁(осн)+S₂(бок)
S₁=(2a)²=4a²
S₂= 4•S∆MAB=4•MH•AB:2=8a²
S(полн)=12а²
12а²=108⇒ а²=9⇒
а=3⇒
АВ=2а=6 см
Формула объема пирамиды
V=S•h:3
S=36
V=36•3√3:3=36√3 см³