В равнобедренном треугольнике ABC угол B равен 110 градусов. Определите угол между прямой, содержащей высоту AA1, и прямой, содержащей биссектрису BB1. ответ запишите в градусах.
Объяснение:
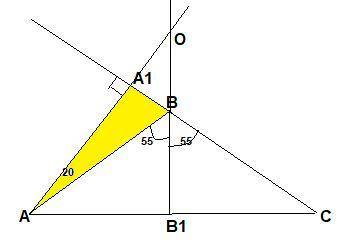
Высота АА₁ падает на продолжение стороны ВС, т.к ∠АВС тупой. Тогда углом между между прямой, содержащей высоту AA₁, и прямой, содержащей биссектрису BB₁ будет∠АОВ₁ .
Угол АВС внешний для Δ АВА₁, значит ∠ВАА₁=110°-90°=20°.
ΔАВС-равнобедренный, углы при основании равны
∠ВАС=(180-110°):2=35° → ∠В₁АО=35°+20°=55°.
Δ АОВ₁ -прямоугольный , ∠АОВ₁=90°-55°=35°
ВD=корень (68-24корень6) см
АС=корень (68+24корень6) см
Объяснение:
АВСD - параллелограмм
СD=6 cм
АD=4корень2 см
<С=30 см
Найти : АС ; ВD
АВ=СD=6 см
AD=BC=4корень2 см
<A=<C=30 градусов
<B=<D=180-30=150 градусов
ВD=корень(CD^2+BC^2-2×CD×BC×cosC)=
=корень(6^2+(4корень2)^2-
-2×6×4корень2×(корень3 /2))=
=корень (36+32-24корень6)=
=корень (68-24корень6) см
АС=корень(АD^2+CD^2-2×AD×CD×cos150)=
=корень((4корень2) ^2+6^2-
-2×(4корень2) ×6×(-корень3/2)) =
=корень(32+36+24корень6) =
=корень (68+24корень6) см
Я сама не знаю даже